题目内容
12.已知(x+y)2=1,x2+y2=25,求①xy的值;②x-y的值.
分析 根据完全平方公式即可求出答案.
解答 解:①∵(x+y)2=1,x2+y2=25,
∴x2+2xy+y2=1,
∴25+2xy=1,
∴xy=-12
②∵(x-y)2=x2-2xy+y2,
∴(x-y)2=25+24=49,
∴x-y=±7
点评 本题考查完全平方公式,解题的关键是熟练运用完全平方公式,本题属于基础题型.

练习册系列答案
相关题目
2.下列各式:①a;②$\frac{{-4x{y^2}}}{3}$;③x2-$\frac{1}{x}$+1;④0;⑤3+4y;⑥-$\frac{{2({x-y})}}{3}$中,其中是多项式的有( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
20.一种商品按销售量分三部分制定销售单价,如表:
(1)若买100件花250元,买300件花690元;买350件花790元;
(2)小明买这种商品花了338元,列方程求购买这种商品多少件?
(3)若小明花了n元(n>250),恰好购买0.45n件这种商品,求n的值.
| 销售量 | 单价 |
| 不超过100件的部分 | 2.5元/件 |
| 超过100件不超过300件的部分 | 2.2元/件 |
| 超过300件的部分 | 2元/件 |
(2)小明买这种商品花了338元,列方程求购买这种商品多少件?
(3)若小明花了n元(n>250),恰好购买0.45n件这种商品,求n的值.
4.已知|2x+3|=-2x-3,则x的取值范围是( )
| A. | x>-$\frac{3}{2}$ | B. | x<-$\frac{3}{2}$ | C. | x≥-$\frac{3}{2}$ | D. | x≤-$\frac{3}{2}$ |
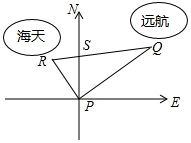 某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定的方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{1}{2}$小时后相距10海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
某港口位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定的方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口$\frac{1}{2}$小时后相距10海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
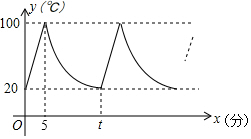 如图所示,小明家饮水机中原有水的温度是20℃,开机通电后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系.当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系.当水温降至20℃时,饮水机又自动开始加热…,不断重复上述程序.根据图中提供的信息,解答下列问题:
如图所示,小明家饮水机中原有水的温度是20℃,开机通电后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系.当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系.当水温降至20℃时,饮水机又自动开始加热…,不断重复上述程序.根据图中提供的信息,解答下列问题: