题目内容
18．
已知：如图，△ABC内接于⊙O，AB=AC，D为BC上任意一点，连接AD，BD，求证：∠ABD=∠AEB．
分析 根据等腰三角形的性质得到∠ABC=∠C，根据同圆中相同的弦所对圆周角相等得到∠DAC=∠CBD，再根据三角形外角的性质和等量关系即可求解．
解答 证明：∵AB=AC，
∴∠ABC=∠C，
∵∠DAC=∠CBD，
∠ABD=∠ABC+∠CBD，∠AEB=∠C+∠DAC，
∴∠ABD=∠AEB．
点评 此题考查了等腰三角形的性质，圆周角定理，关键是得到∠ABC=∠C，∠DAC=∠CBD．
练习册系列答案
相关题目
如图，阴影部分的面积是ab-$\frac{π{a}^{2}}{4}$（用含字母a，b的式子表示）．
如图，矩形ABCD的对角线相交于点O，AB=4cm，∠AOB=60°．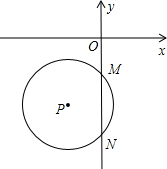
如图，半径为5的⊙P与y轴相交于点M（0，-4）和N（0，-10），以P为顶点的抛物线经过点M，求抛物线的解析式．
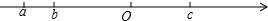有理数a，b，c在数轴上的位置如图所示，试化简|a-b|-|c-a|+|b-c|-|a|．
4．
如图，将腰长为$\sqrt{2}$cm的等腰直角三角形ABC绕点B旋转到△A'B'C'位置，使A、B、C'三点在同一直线上，则点A经过的路线长是（ ）
如图，将腰长为$\sqrt{2}$cm的等腰直角三角形ABC绕点B旋转到△A'B'C'位置，使A、B、C'三点在同一直线上，则点A经过的路线长是（ ）| A． | $\frac{3}{4}$πcm | B． | $\frac{3}{4}$$\sqrt{2}$πcm | C． | $\frac{3}{2}$πcm | D． | $\frac{1}{2}$π |