题目内容
6. 如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.(1)按如图所示建立平面直角坐标系,求表示该抛物线的函数表达式;
(2)一辆货运卡车高为4m,宽为2m,如果该隧道内设双向车道,那么这辆货车能否安全通过?
分析 (1)根据题意可知顶点坐标和点B坐标,设抛物线的函数表达式为顶点式,代入即可求出表达式;
(2)利用宽2m求高为5m,所以可以通过.
解答 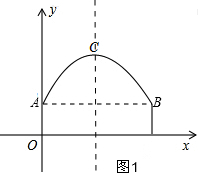 解:(1)如图1,由题意得:最高点C(4,6),B(8,2),
解:(1)如图1,由题意得:最高点C(4,6),B(8,2),
设抛物线的函数表达式:y=a(x-4)2+6,
把(8,2)代入得:a(8-4)2+6=2,
a=-$\frac{1}{4}$,
∴y=-$\frac{1}{4}$(x-4)2+6;
(2)如图2,当DE=2时,
AD=AE-DE=4-2=2,
当x=2时,y=-$\frac{1}{4}$(2-4)2+6=5>4,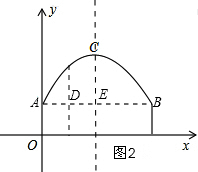
∴这辆货车能安全通过.
点评 本题是二次函数的应用,属于抛物线型隧道或拱桥问题,此类题一般函数表达式求法比较简单,但若货运卡车等是否能通过隧道问题,有两种情况:单向车道或双向车道,要仔细审题,可以利用宽来计算高,也可以利用高来计算宽,把对应的坐标代入即可.

练习册系列答案
相关题目
17.若$\frac{1}{x}$-$\frac{1}{y}$=2,则$\frac{3x+xy-3y}{x-xy-y}$的值为( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | -$\frac{5}{3}$ | D. | $\frac{5}{3}$ |
 如图,在△ABE中,已知AB=AE,AD=AC,∠1=∠2,那么△ABC与△AED全等吗?说明理由?
如图,在△ABE中,已知AB=AE,AD=AC,∠1=∠2,那么△ABC与△AED全等吗?说明理由?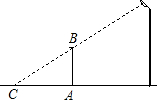 如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④.
如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC﹙假定AC>AB﹚,影长的最大值为m,最小值为n,那么下列结论中:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.正确的结论序号是①③④. 如图,A,F,E,B四点在同一直线上,AC⊥CE,BD⊥DF,AF=BE,AC=BD.试判断DF与CE的关系(指数量与位置关系),并说明理由.
如图,A,F,E,B四点在同一直线上,AC⊥CE,BD⊥DF,AF=BE,AC=BD.试判断DF与CE的关系(指数量与位置关系),并说明理由.