题目内容
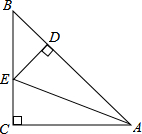 如图,Rt△ABC,BC=AC,∠C=90°,AE平分∠BAC,且ED⊥AB于D,求证:EC=BD.
如图,Rt△ABC,BC=AC,∠C=90°,AE平分∠BAC,且ED⊥AB于D,求证:EC=BD.考点:角平分线的性质,等腰直角三角形
专题:证明题
分析:先求出△ABC是等腰直角三角形,根据等腰直角三角形的性质可得∠B=45°,再求出△BDE是等腰直角三角形,根据等腰直角三角形的性质可得BD=DE,然后根据角平分线上的点到角的两边距离相等可得EC=DE,然后等量代换即可得证.
解答:证明:∵BC=AC,∠C=90°,
∴△ABC是等腰直角三角形,
∴∠B=45°,
∵ED⊥AB,
∴△BDE是等腰直角三角形,
∴BD=DE,
∵∠C=90°,AE平分∠BAC,ED⊥AB,
∴EC=DE,
∴EC=BD.
∴△ABC是等腰直角三角形,
∴∠B=45°,
∵ED⊥AB,
∴△BDE是等腰直角三角形,
∴BD=DE,
∵∠C=90°,AE平分∠BAC,ED⊥AB,
∴EC=DE,
∴EC=BD.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,等腰直角三角形的判定与性质,熟记性质并判断出等腰直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知△ABC中,∠ACB=90°,AC=BC,AD=DC,求sin∠ABD的值.
已知△ABC中,∠ACB=90°,AC=BC,AD=DC,求sin∠ABD的值. 如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D=
如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D= 已知:如图,函数y1=ax的图象与函数y2=
已知:如图,函数y1=ax的图象与函数y2=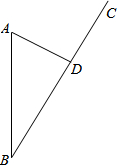 今年第九号台风“苏拉”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向85km的B处,正以14km/h的速度沿BC方向移动.已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?(计算结果精确到0.1小时)
今年第九号台风“苏拉”登陆浙江,A市接到台风警报时,台风中心位于A市正南方向85km的B处,正以14km/h的速度沿BC方向移动.已知A市到BC的距离AD=40km,那么台风中心从B点移到D点经过多长时间?(计算结果精确到0.1小时) 如图,OA=OC,已知tan∠AOC=
如图,OA=OC,已知tan∠AOC=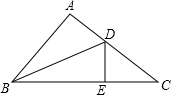 如图,BD是△ABC的角平分线,DE⊥BC于E,若S△ABC=60cm2,AB=12cm,BC=18cm,则S△DBC=
如图,BD是△ABC的角平分线,DE⊥BC于E,若S△ABC=60cm2,AB=12cm,BC=18cm,则S△DBC=