题目内容
 如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D=
如图,若CD平分∠ACE,BD平分∠ABC,∠A=45°,则∠D=考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线定义求出∠ABC=2∠DBC,∠ACE=2∠DCE,根据三角形外角性质求出∠ACE=2∠DCE=∠A+∠ABC,2∠DCE=2(∠D+∠DBC)=2∠D+∠ABC,推出∠A+∠ABC=2∠D+∠ABC,得出∠A=2∠D,即可求出答案.
解答:解:∵BD平分∠ABC,CD平分∠ACE,
∴∠ABC=2∠DBC,∠ACE=2∠DCE,
∵∠ACE=2∠DCE=∠A+∠ABC,2∠DCE=2(∠D+∠DBC)=2∠D+∠ABC,
∴∠A+∠ABC=2∠D+∠ABC,
∴∠A=2∠D,
∵∠A=45°,
∴∠D=22.5°,
故答案为:22.5.
∴∠ABC=2∠DBC,∠ACE=2∠DCE,
∵∠ACE=2∠DCE=∠A+∠ABC,2∠DCE=2(∠D+∠DBC)=2∠D+∠ABC,
∴∠A+∠ABC=2∠D+∠ABC,
∴∠A=2∠D,
∵∠A=45°,
∴∠D=22.5°,
故答案为:22.5.
点评:本题考查了三角形外角性质,角平分线定义的应用,关键是推出∠A=2∠D.

练习册系列答案
相关题目
在抛物线y=x2-4x-4上的一个点是( )
| A、(4,4) | ||||
| B、(3,-1) | ||||
| C、(-2,-8) | ||||
D、(-
|
已知点(x1,-1),(x2,-
),(x3,2)三点都在函数y=
的图象上,则下列关系式正确的是( )
| 1 |
| 2 |
| 4 |
| x |
| A、x3>x2>x1 |
| B、x1>x2>x3 |
| C、x1>x3>x2 |
| D、x3>x1>x2 |


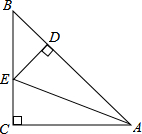 如图,Rt△ABC,BC=AC,∠C=90°,AE平分∠BAC,且ED⊥AB于D,求证:EC=BD.
如图,Rt△ABC,BC=AC,∠C=90°,AE平分∠BAC,且ED⊥AB于D,求证:EC=BD.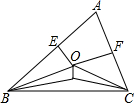 OE,OF分别是AB,AC边的中垂线,∠OBC,∠OCB的平分线相交于点I,试分析OI与BC位置关系,并给出证明.
OE,OF分别是AB,AC边的中垂线,∠OBC,∠OCB的平分线相交于点I,试分析OI与BC位置关系,并给出证明.