题目内容
10．化简求值：$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$+$\frac{2a-{a}^{2}}{a-2}$÷a，其中a=-2．分析 先把分子分母因式分解和除法运算化为乘法运算，再约分后进行通分，然后进行同分母的减法运算得到原式=$\frac{2}{a-1}$，再把a的值代入计算即可．
解答 解：原式=$\frac{（a+1）（a-1）}{（a-1）^{2}}$+$\frac{-a（a-2）}{a-2}$•$\frac{1}{a}$
=$\frac{a+1}{a-1}$-1
=$\frac{a+1-（a-1）}{a-1}$
=$\frac{2}{a-1}$，
当a=-2时，原式=$\frac{2}{-2-1}$=-$\frac{2}{3}$．
点评 本题考查了分式的化简求值：先把分式化简后，再把分式中未知数对应的值代入求出分式的值．在化简的过程中要注意运算顺序和分式的化简．化简的最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．
练习册系列答案
相关题目
如图，将矩形纸片P折叠，使点A与点C重合，折痕为EF，若AB=8，BC=4．则：
18．
如图，⊙O的半径是5，AB是⊙O的直径，弦CD⊥AB，垂足为P，若CD=8，则△ACD的面积是（ ）
如图，⊙O的半径是5，AB是⊙O的直径，弦CD⊥AB，垂足为P，若CD=8，则△ACD的面积是（ ）| A． | 16 | B． | 24 | C． | 32 | D． | 48 |
15．
如图为4×4的网格图，A，B，C，D，O均在格点上，点O是（ ）
如图为4×4的网格图，A，B，C，D，O均在格点上，点O是（ ）| A． | △ACD的外心 | B． | △ABC的外心 | C． | △ACD的内心 | D． | △ABC的内心 |
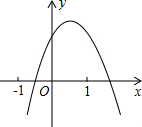二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①b＜0；②c＞0；③a+c＜b；④b2-4ac＞0，其中正确的个数是（ ）