题目内容
16.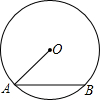 如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )
如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )| A. | $\frac{{4\sqrt{5}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{3}$ | C. | 4 | D. | $\frac{{2\sqrt{5}}}{3}$ |
分析 作OD垂直AB于D.根据垂径定理和勾股定理求解.
解答  解:作OD垂直AB于D.
解:作OD垂直AB于D.
∵OA=2,sinA=$\frac{2}{3}$,
∴OD=OA•sinA=2×$\frac{2}{3}$=$\frac{4}{3}$.
∴AD=$\sqrt{{OA}^{2}-{OD}^{2}}$=$\sqrt{{2}^{2}-{(\frac{4}{3})}^{2}}$=$\frac{2\sqrt{5}}{3}$,
∴AB=2AD=$\frac{4\sqrt{5}}{3}$.
故选A.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,长方形ABCD中,长BC=a,宽AB=b,(b<a<2b),四边形ABEH和四边形ECGF都是正方形.
如图,长方形ABCD中,长BC=a,宽AB=b,(b<a<2b),四边形ABEH和四边形ECGF都是正方形.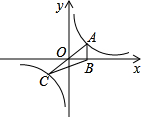 如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{4}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于4.
如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{4}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于4.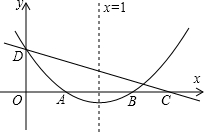 如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于AB两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确的个数是( )
如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x轴交于AB两点,其对称轴为直线x=1,且OA=OD,直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确的个数是( )