题目内容
4.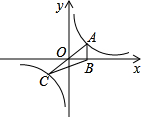 如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{4}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于4.
如图,正比例函数y=kx(k>0)与反比例函数y=$\frac{4}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连接BC,则△ABC的面积等于4.
分析 设点A坐标(x,kx),根据点A,C关于原点对称,可得出点C坐标,再根据三角形的面积计算即可.
解答 解:点A坐标(x,kx),
∴点C坐标(-x,-kx),
∵AB⊥x轴,
∴S△ABC=$\frac{1}{2}$AB•(0B-x)=$\frac{1}{2}$×kx×2x=kx2,
∵比例函数y=kx(k>0)与反比例函数y=$\frac{4}{x}$的图象相交于A、C两点,
∴kx2=4,
∴S△ABC=4.
故答案为4.
点评 本题考查了一次函数与反比例函数的交点问题,三角形的面积,解方程组等知识点,主要考查学生的计算能力,题目比较好.

练习册系列答案
相关题目
14.∠A=125°12′,则它的补角为( )
| A. | 75°48′ | B. | 54°48′ | C. | 35°48′ | D. | 25°12′ |
16.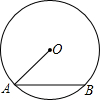 如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )
如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )
 如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )
如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )| A. | $\frac{{4\sqrt{5}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{3}$ | C. | 4 | D. | $\frac{{2\sqrt{5}}}{3}$ |
 如图,二次函数y=ax2+bx+c的图象经过点($\frac{1}{2}$,0),对称轴为x=-1,下列5个结论:①abc>0;②a+2b+4c=0;③2a-b>0;④3b+2c>0;⑤a-b≥m(ma+b)(m为任意实数),其中正确结论的个数是( )
如图,二次函数y=ax2+bx+c的图象经过点($\frac{1}{2}$,0),对称轴为x=-1,下列5个结论:①abc>0;②a+2b+4c=0;③2a-b>0;④3b+2c>0;⑤a-b≥m(ma+b)(m为任意实数),其中正确结论的个数是( )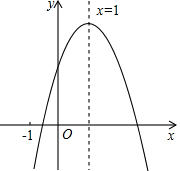 二次函数y=ax2+bx+c的图象如图所示,有下列4个结论:
二次函数y=ax2+bx+c的图象如图所示,有下列4个结论: