题目内容
8.某市在美化工程招标时,接到甲、乙两个工程队投标书,甲队施工一天,需付工程款3.5万元,乙队施工一天,需压工程款2万元,工程领导小组根据甲、乙两队的投标书测算,有如下方案:(1)甲队单独做完成这项工程刚好如期完成;
(2)乙队单独做完成这项工程要比规定日期多用5天;
(3)若甲乙两队先合做4天,剩下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
分析 设规定的时间是x天,则乙单独完成需要(x+5)天,由工程问题的数量关系建立方程求出甲、乙单独完成需要的时间,就可以求出每种方案的费用,再比较大小即可求出结论.
解答 解:设规定的时间是x天,则乙单独完成需要(x+5)天,由题意,得
$\frac{4}{x}+\frac{x}{x+5}=1$,
解得;x=20.
经检验,x=20是元方程的根.
∴乙队单独完成需要的时间是20+5=25天.
方案1,甲队单独完成需要的费用是:3.5×20=70万元,
方案3,甲乙两队先合做4天,剩下的工程由乙队单独做的费用为:3.5×4+20×2=54(万元).
∵70>54,
∴在不耽误工期的前提下,方案3,甲乙两队先合做4天,剩下的工程由乙队单独做最节省工程款.
点评 本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,工程问题的数量关系工作总量÷工作效率=工作时间的运用,解答时由工程问题的数量关系建立方程求出甲、乙单独完成需要的时间是关键.

练习册系列答案
相关题目
16.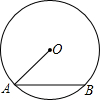 如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )
如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )
 如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )
如图,AB是⊙O的弦,半径OA=2,sinA=$\frac{2}{3}$,则弦AB的长为( )| A. | $\frac{{4\sqrt{5}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{3}$ | C. | 4 | D. | $\frac{{2\sqrt{5}}}{3}$ |
17.下列说法中正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后3点朝上是不可能事件 | |
| B. | 了解一批电视机的使用寿命,适合用抽样调查的方式 | |
| C. | 若a为实数,则|a|>0是必然事件 | |
| D. | 甲、乙两人各进行10次射击,两人射击成绩的方差分别为S${\;}_{甲}^{2}$=2,S${\;}_{乙}^{2}$=4,则乙的射击成绩更稳定 |
18. 某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
频数分布表
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
 某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:频数分布表
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 4 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
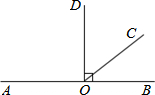 如图,O是直线AB上一点,OC是一条射线,OD垂直直线AB,且∠AOC-∠BOC=32°,
如图,O是直线AB上一点,OC是一条射线,OD垂直直线AB,且∠AOC-∠BOC=32°, 如图,二次函数y=ax2+bx+c的图象经过点($\frac{1}{2}$,0),对称轴为x=-1,下列5个结论:①abc>0;②a+2b+4c=0;③2a-b>0;④3b+2c>0;⑤a-b≥m(ma+b)(m为任意实数),其中正确结论的个数是( )
如图,二次函数y=ax2+bx+c的图象经过点($\frac{1}{2}$,0),对称轴为x=-1,下列5个结论:①abc>0;②a+2b+4c=0;③2a-b>0;④3b+2c>0;⑤a-b≥m(ma+b)(m为任意实数),其中正确结论的个数是( )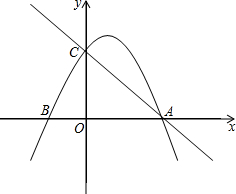 如图,抛物线y=$\frac{1}{k}$(x-2)(x-k)与x轴交于A,B两点,与y轴交于点C.
如图,抛物线y=$\frac{1}{k}$(x-2)(x-k)与x轴交于A,B两点,与y轴交于点C.