题目内容
9.如图,△ABC和△AED是等腰直角三角形,∠BAC=∠EAD=90°,点D、E在∠BAC的外部,连结DC、BE.(1)求证:BE=CD;
(2)若将△AED绕点A旋转,直线CD交直线AB于点G,交直线BE于点K.若AC=8,GA=2,试求GC•KG的值.
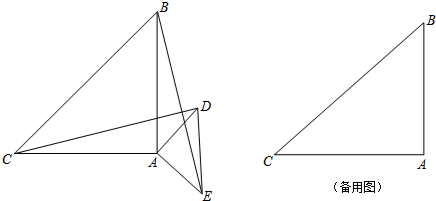
分析 (1)根据∠BAC=∠EAD=90°,得出∠CAD=∠BAE,在△BAE和△CAD中,根据SAS得出△BAE≌△CAD,即可证出BE=CD;
(2)当点G在线段AB上时,根据(1)和AA得出△CGA∽△BGK,求出AG•GB=GC•KG,再根据AC=8,GA=2,得出GC•KG=12;当点G在线段AB延长线上时,再根据已知条件求出△CGA∽△BGK,得出AG•GB=GC•KG,再根据AC=8,GA=2,得出GC•KG=20;
解答 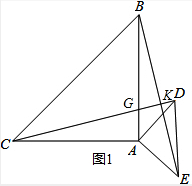 解:(1)∵∠BAC=∠EAD=90°
解:(1)∵∠BAC=∠EAD=90°
∴∠BAC+∠BAD=∠EAD+∠BAD,
∴∠CAD=∠BAE,
在△BAE和△CAD中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAD}\\{AE=AD}\end{array}\right.$,
∴△BAE≌△CAD(SAS),
∴BE=CD;
(2)当点G在线段AB上时(如图1)
∵△BAE≌△CAD,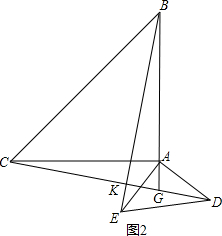
∴∠ACD=∠ABE,
又∵∠CGA=∠BGK,
∴△CGA∽△BGK,
∴$\frac{AG}{KG}$=$\frac{GC}{GB}$,
∴AG•GB=GC•KG,
∵AC=8,
∴AB=8,
∵GA=2,
∴GB=6.
∴GC•KG=12,
当点G在线段AB延长线上时(如图2)
∵△BAE≌△CAD
∴∠ACD=∠ABE,
又∵∠BGK=∠CGA,
∴△CGA∽△BGK,
∴$\frac{AG}{KG}$=$\frac{CG}{GB}$,
∴AG•GB=GC•KG;
∵AC=8,
∴AB=8,
∵GA=2,
∴GB=10
∴GC•KG=20.
点评 此题考查了相似形的综合,用到的知识点是全等三角形的判定与性质、相似三角形的判定与性质、等腰直角三角形的性质,解题的关键是能画出图形.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
20. 如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )
如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )
 如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )
如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )| A. | 互余 | B. | 互补 | C. | 相等 | D. | 不能确定 |
19.下列运算正确的是( )
| A. | 2a2+a=3a3 | B. | a2÷a=a | C. | (-a)3•a2=-a6 | D. | (3a2)3=9a6 |
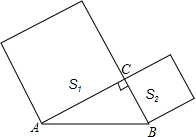 如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为边向外作正方形,面积分别记为S1,S2,则S1+S2的值等于16.
如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为边向外作正方形,面积分别记为S1,S2,则S1+S2的值等于16.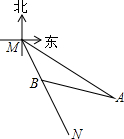 如图,已知射线MN表示一艘轮船的航线路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里.
如图,已知射线MN表示一艘轮船的航线路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为80海里.