题目内容
11. 在平面直角坐标系中,A(0,2),B(4,0),C(4,3)
在平面直角坐标系中,A(0,2),B(4,0),C(4,3)(1)求△ABC的面积;
(2)如果在第二象限内有一点P(a,1),试用含a的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)画出图形,根据三角形面积公式计算即可.
(2)根据S四边形ABCD=S△AOB+S△AOP计算即可,注意a<0这个条件.
(3)列出方程即可解决.
解答 解:(1)如图所示,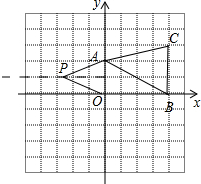
S△ABC=$\frac{1}{2}$×3×4=6.
(2)S四边形ABCD=S△AOB+S△AOP=$\frac{1}{2}$×4×2+$\frac{1}{2}$×2×(-a)=4-a.
(3)由题意4-a=6,
∴a=-2,
∴点p坐标为(-2,1).
点评 本题考查坐标与图形性质、三角形面积等知识,解题的关键是记住三角形面积公式,学会利用分割法求四边形面积,属于中考常考题型.

练习册系列答案
相关题目
19.下列方程中,不是一元二次方程的是( )
| A. | x2=-3 | B. | -4x2+2x+1=0 | C. | 3x2-2x+1=0 | D. | x2+x=(x+1)(x-2) |
6.下列结论错误的是( )
| A. | 垂直于同一直线的两条直线互相平行 | |
| B. | 两直线平行,同旁内角互补 | |
| C. | 过直线外一点有且只有一条直线与这条直线平行 | |
| D. | 同一平面内,不相交的两条直线叫做平行线 |
20. 如图,若AB∥CD,则∠1+∠2+∠3的值为( )
如图,若AB∥CD,则∠1+∠2+∠3的值为( )
 如图,若AB∥CD,则∠1+∠2+∠3的值为( )
如图,若AB∥CD,则∠1+∠2+∠3的值为( )| A. | 90° | B. | 180° | C. | 210° | D. | 270° |
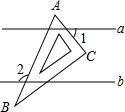 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°),按如图所示放置,若∠1=55°,则∠2的度数为115°.
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°),按如图所示放置,若∠1=55°,则∠2的度数为115°.