题目内容
3.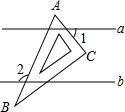 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°),按如图所示放置,若∠1=55°,则∠2的度数为115°.
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°),按如图所示放置,若∠1=55°,则∠2的度数为115°.
分析 直接利用三角形内角和定理结合对顶角的定义得出∠4的度数,再利用平行线的性质得出∠2的度数.
解答  解:∵∠1=55°,∠A=60°,
解:∵∠1=55°,∠A=60°,
∴∠3=∠4=65°,
∵a∥b,
∴∠4+∠2=180°,
∴∠2=115°.
故答案为:115°.
点评 此题主要考查了平行线的性质以及对顶角的定义,正确得出∠4的度数是解题关键.

练习册系列答案
相关题目
18.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )

| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
18.把$\sqrt{1.5}$化成最简二次根式为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
8.下列平面直角坐标系中的图象,不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
15.下列式子可以用平方差公式计算的是( )
| A. | (x-4)(4-x) | B. | (-a-3)(3-a) | C. | (a+b)(-a-b) | D. | (2y-4)(-4+2y) |
13.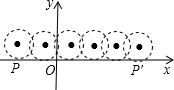 如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )
如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )
 如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )
如图,半径为1个单位长度的圆从点P(-2,0)沿x轴向右滚动一周,圆上的一点由P点到达P′点,则点P′的横坐标是( )| A. | 4 | B. | 2π | C. | π-2 | D. | 2π-2 |
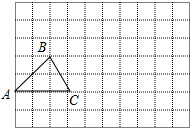 在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上.
在如图所示的方格中,每个小方格都是边长为1的正方形,△ABC的三个顶点都在格点上. 在平面直角坐标系中,A(0,2),B(4,0),C(4,3)
在平面直角坐标系中,A(0,2),B(4,0),C(4,3) 如图,将Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,使AB′恰好经过点C,连接BB′,则∠BAC′的度数为80°.
如图,将Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,使AB′恰好经过点C,连接BB′,则∠BAC′的度数为80°.