Question

13．证明与操作
（1）请证明：在同一平面内，如果两条直线都垂直于同一直线，那么这两条直线平行；
（2）如图是一个四边形的纸片ABCD，E是纸片上一点，请你只能通过折叠，过点E作出一条折痕MN与AB平行，并作适当的文字说明；
（3）作一个三角形，使它的面积等于（2）中四边形的纸片ABCD的面积，并作适当的文字说明．

Answer 1

分析 （1）根据题意画出图形，进而可得出结论；
（2）过点D作DF⊥AB，再过点E作EG⊥DF，延长AE分别交AD、BC于点MN，则直线MN即为所求；
（3）连接BD，过点C作CE∥BD交AD的延长线与点E，则△ABE即为所求．

解答 （1）证明：如图，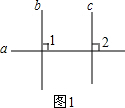

∵b⊥a，c⊥a，
∴∠1=∠2=90°，
∴b∥c，即在同一平面内，如果两条直线都垂直于同一直线，那么这两条直线平行；

（2）解：如图2所示；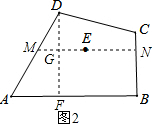

过点D作DF⊥AB，再过点E作EG⊥DF，延长AE分别交AD、BC于点MN，则直线MN即为所求；

（3）解：如图3所示，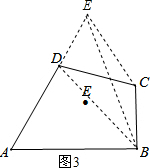

连接BD，过点C作CE∥BD交AD的延长线与点E，
∵△BDE与△BDC同底等高，
∴S_△BDE=S_△BDC，
∴S_{四边形ABCD}=S_△ABE．

点评 本题考查的是翻折变换，熟知图形翻折不变性的性质是解答此题的关键．