题目内容
 如图,已知AB是⊙O的直径,BC、EF是⊙O的弦,且EF垂直AB于点G,交BC于点H,CD与FE延长线交于D点,CD=DH.
如图,已知AB是⊙O的直径,BC、EF是⊙O的弦,且EF垂直AB于点G,交BC于点H,CD与FE延长线交于D点,CD=DH.(1)求证:CD是⊙O的切线;
(2)若H为BC中点,AB=10,EF=8,求CD的长.
考点:切线的判定
专题:
分析:(1)要求证:DC是圆O的切线,只要证明OC⊥PC即可.
(2)AB与EF是两条相交的弦,根据相交弦定理得到AG•BG=EG2即(AB-BG)BE=16即BG2-10BG+16=0,就可以求出BG的长.进而求出BC,就可以求出sinA的值.
(2)AB与EF是两条相交的弦,根据相交弦定理得到AG•BG=EG2即(AB-BG)BE=16即BG2-10BG+16=0,就可以求出BG的长.进而求出BC,就可以求出sinA的值.
解答: 解:(1)连接OD、OC相交于M,
解:(1)连接OD、OC相交于M,
∵∠ACB=90°,CO=AO,
∴∠ACO=∠CAO,∠CAO+∠B=90°,∠B+∠BHG=90°.
∴∠CAO=∠BHG.
∵DC=DH,
∴∠DCH=∠DHC.
∴∠DCH=∠ACO.
∴∠DCH+∠HCO=∠ACO+∠OCH=90°.
∴OC⊥PC.
即DC为切线.
(2)∵AB=10,EF=8,EF垂直AB,
∴EG=4=GF.
∴OG=3,
∴BG=2.
连接OH,
∵H为BC中点,
∴OH⊥BC,
∴△BHG∽△BHG,
∴BH2=BG•BO=2×5=10,
∴BH=
=CH,
同理得:HG=
,
cos∠BHG=
=
=
.
又∵∠DCH=∠DHC=∠BHG,
∴
=cos∠DCB=cos∠BHG=
,
∴CD=
.
 解:(1)连接OD、OC相交于M,
解:(1)连接OD、OC相交于M,∵∠ACB=90°,CO=AO,
∴∠ACO=∠CAO,∠CAO+∠B=90°,∠B+∠BHG=90°.
∴∠CAO=∠BHG.
∵DC=DH,
∴∠DCH=∠DHC.
∴∠DCH=∠ACO.
∴∠DCH+∠HCO=∠ACO+∠OCH=90°.
∴OC⊥PC.
即DC为切线.
(2)∵AB=10,EF=8,EF垂直AB,
∴EG=4=GF.
∴OG=3,
∴BG=2.
连接OH,
∵H为BC中点,
∴OH⊥BC,
∴△BHG∽△BHG,
∴BH2=BG•BO=2×5=10,
∴BH=
| 10 |
同理得:HG=
| 6 |
cos∠BHG=
| HG |
| BH |
| ||
|
| ||
| 5 |
又∵∠DCH=∠DHC=∠BHG,
∴
| ||
| CD |
| ||
| 5 |
∴CD=
5
| ||
| 6 |
点评:考查了切线的判定.证明一条直线是圆的切线,只要证明直线经过半径的外端点,且垂直于这条半径就可以.证明线段的积相等的问题可以转化为三角形相似的问题.

练习册系列答案
相关题目

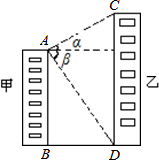 如图甲楼AB的高为40米,小华从甲楼顶A测乙楼顶C仰角为α=30°,观测乙楼的底部D俯角为β=45°;
如图甲楼AB的高为40米,小华从甲楼顶A测乙楼顶C仰角为α=30°,观测乙楼的底部D俯角为β=45°;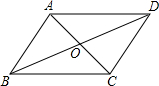 如图,在四边形ABCD中,AD∥BC,AC、BD相交于点O,请你添加一对线段或一对角之间关系的条件,使四边形ABCD是平行四边形,你所添加的条件是
如图,在四边形ABCD中,AD∥BC,AC、BD相交于点O,请你添加一对线段或一对角之间关系的条件,使四边形ABCD是平行四边形,你所添加的条件是