题目内容
某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路,若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是
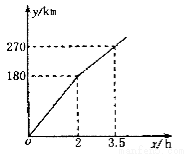
A. 汽车在高速公路上行驶速度为100km/h
B. 乡村公路总长为90km
C. 汽车在乡村公路上行驶速度为60km/h
D. 该记者在出发后4.5h到达采访地
 C
【解析】
试题分析:若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,由图得汽车在高速公路上行驶速度为,所以A错误;乡村公路总长=360km-180km=180km,所以B错误;汽车在乡村公路上行驶速度,所以C正确;该记者在出发后到达采访地的时间=在高速公路和乡村公路上行驶时间之和=2+=2+3=5
C
【解析】
试题分析:若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,由图得汽车在高速公路上行驶速度为,所以A错误;乡村公路总长=360km-180km=180km,所以B错误;汽车在乡村公路上行驶速度,所以C正确;该记者在出发后到达采访地的时间=在高速公路和乡村公路上行驶时间之和=2+=2+3=5
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则;等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化成整式与真分式的和的形式,如: 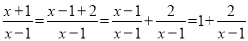 ;
; 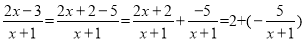
(1)下列分式中,属于真分式的是:________(填序号);
①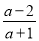 ②
②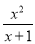 ③
③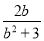 ④
④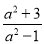
(2)将假分式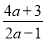 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: 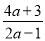 =________+________;
=________+________;
(3)将假分式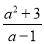 化成整式与真分式的和的形式:
化成整式与真分式的和的形式: 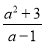 =__________________.
=__________________.
 (1)③;(2)2, ;(3)a+1+ .
【解析】试题分析:(1)认真阅读题意,体会真分式的特点,然后判断即可;
(2)根据题意的化简方法进行化简即可;
(3)根据题意的化简方法进行化简即可.
试题解析:(1)①中的分子分母均为1次,②中分子次数大于分母次数,③分子次数小于分母次数,④分子分母次数一样,故选③.
(2)=,故答案为:2, ;
(3)== ,故答...
(1)③;(2)2, ;(3)a+1+ .
【解析】试题分析:(1)认真阅读题意,体会真分式的特点,然后判断即可;
(2)根据题意的化简方法进行化简即可;
(3)根据题意的化简方法进行化简即可.
试题解析:(1)①中的分子分母均为1次,②中分子次数大于分母次数,③分子次数小于分母次数,④分子分母次数一样,故选③.
(2)=,故答案为:2, ;
(3)== ,故答... 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
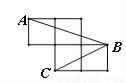
 【解析】
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值.
【解析】
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值. 在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍 B.都缩小两倍 C.不变 D.都扩大四倍
 C
【解析】
试题分析:根据三边对应成比例,两三角形相似,可知扩大后的三角形与原三角形相似,再根据相似三角形对应角相等解答.
【解析】
∵各边的长度都扩大两倍,
∴扩大后的三角形与Rt△ABC相似,
∴锐角A的各三角函数值都不变.
故选C.
C
【解析】
试题分析:根据三边对应成比例,两三角形相似,可知扩大后的三角形与原三角形相似,再根据相似三角形对应角相等解答.
【解析】
∵各边的长度都扩大两倍,
∴扩大后的三角形与Rt△ABC相似,
∴锐角A的各三角函数值都不变.
故选C. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
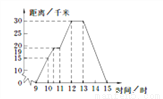
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
 (1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看...
(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看... 如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.

 见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,...
见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
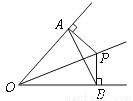
∵PD⊥BC,PE⊥BM,... 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B。下列结论中不一定成立的是( )
A、PA=PB B、PO平分∠AOB
C、OA=OB D、AB垂直平分OP
 D
【解析】
试题分析:本题要从已知条件OP平分∠AOB入手,利用角平分线的性质:因OP平分∠AOB,PA⊥OA,PB⊥OB,得到PA=PB,进而推出△AOE≌△BOE,从未得到∠APO=∠BPO,OA=OB,因此A、B、C项正确;设PO与AB相交于E,由OA=OB,∠AOP=∠BOP,OE=OE,得证△AOE≌△BOE,进而得∠AEO=∠BEO=90°,因此得证OP垂直AB,而不能得...
D
【解析】
试题分析:本题要从已知条件OP平分∠AOB入手,利用角平分线的性质:因OP平分∠AOB,PA⊥OA,PB⊥OB,得到PA=PB,进而推出△AOE≌△BOE,从未得到∠APO=∠BPO,OA=OB,因此A、B、C项正确;设PO与AB相交于E,由OA=OB,∠AOP=∠BOP,OE=OE,得证△AOE≌△BOE,进而得∠AEO=∠BEO=90°,因此得证OP垂直AB,而不能得... 如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的点 处,那么tan∠BAD′等于( )
处,那么tan∠BAD′等于( )
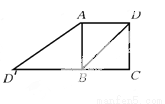
A. 1 B. 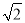 C.
C. 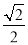 D.
D. 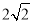
 B
【解析】试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B.
B
【解析】试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B. (3分)必然事件的概率是( )
A.﹣1 B.0 C.0.5 D.1
 D.
【解析】
试题分析:∵必然事件就是一定发生的事件,∴必然事件发生的概率是1.故选D.
D.
【解析】
试题分析:∵必然事件就是一定发生的事件,∴必然事件发生的概率是1.故选D.