题目内容
3．
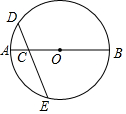如图，C是⊙O的直径AB上一点，过点C作弦DE，使CD=CO，若$\widehat{AD}$的度数为35°，求$\widehat{BE}$的度数．
分析 连接OD、OE，根据圆心角、弧、弦的关系定理求出∠AOD=35°，根据等腰三角形的性质和三角形内角和定理计算即可．
解答 解：
连接OD、OE，
∵$\widehat{AD}$的度数为35°，
∴∠AOD=35°，
∵CD=CO，
∴∠ODC=∠AOD=35°，
∵OD=OE，
∴∠ODC=∠E=35°，
∴∠DOE=110°，
∴∠AOE=75°，
∴∠BOE=105°，
∴$\widehat{BE}$的度数是105°．
点评 本题考查的是圆心角、弧、弦的关系定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．三个数：|-$\frac{7}{8}$|、+（-$\frac{6}{7}$）、-|-1|的大小关系是（ ）
| A． | +（-$\frac{6}{7}$）＜|-$\frac{7}{8}$|＜-|-1| | B． | -|-1|＜|-$\frac{7}{8}$|＜+（-$\frac{6}{7}$） | C． | -|-1|＜+（-$\frac{6}{7}$）＜|-$\frac{7}{8}$| | D． | |-$\frac{7}{8}$|＜+（-$\frac{6}{7}$）＜-|-1| |
12．
如图，数轴上A、B两点分别对应的数为a、b，则下列结论错误的是（ ）
如图，数轴上A、B两点分别对应的数为a、b，则下列结论错误的是（ ）| A． | a+b＜0 | B． | ab＜0 | C． | |b|=b | D． | |a|＜|b| |
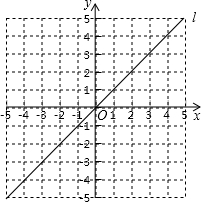如图，在直角坐标系中，已知直线l是第一、三象限的角平分线，点A（2，0），B（3，1）．