题目内容
13.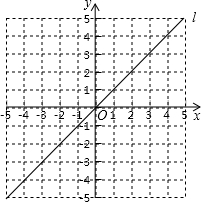 如图,在直角坐标系中,已知直线l是第一、三象限的角平分线,点A(2,0),B(3,1).
如图,在直角坐标系中,已知直线l是第一、三象限的角平分线,点A(2,0),B(3,1).(1)在坐标系中分别描出点A、B及点A、B关于直线l的对称点A′、B′,并写出点A′、B′的坐标;
(2)根据(1)中点A与点A′,点B与B′的坐标特征,在直线l外任取一个点P(m,n),写出该点关于直线l的对称点P′的坐标.
分析 (1)作出各点关于直线l的对称点,并写出各点坐标即可;
(2)根据点A与点A′,点B与B′的坐标特征即可得出结论.
解答  解:(1)如图,由图可知,A′(0,2),B′(1,3);
解:(1)如图,由图可知,A′(0,2),B′(1,3);
(2)∵点A(2,0),B(3,1),A′(0,2),B′(1,3),
∴点P(m,n)关于直线l的对称点P′的坐标为(n,m).
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.抛物线y=x2+1与直线y=kx的交点A的横坐标是1,则关于x的不等式x2+kx-3<0的解集是( )
| A. | x>1 | B. | x<-3 | C. | -3<x<1 | D. | -1<x<3 |
18. 如图,在△ABC与△DEF中,B、F、C、E在一条直线上,若BF=CE,AC=FD,则下列补充的条件能说明△ABC≌△DEF的有( )
如图,在△ABC与△DEF中,B、F、C、E在一条直线上,若BF=CE,AC=FD,则下列补充的条件能说明△ABC≌△DEF的有( )
①∠E=∠B; ②AC∥DF; ③∠A=∠D.
 如图,在△ABC与△DEF中,B、F、C、E在一条直线上,若BF=CE,AC=FD,则下列补充的条件能说明△ABC≌△DEF的有( )
如图,在△ABC与△DEF中,B、F、C、E在一条直线上,若BF=CE,AC=FD,则下列补充的条件能说明△ABC≌△DEF的有( )①∠E=∠B; ②AC∥DF; ③∠A=∠D.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
5.计算(-3)-(-7)的结果为( )
| A. | -10 | B. | -4 | C. | 4 | D. | 10 |
3.十位数字是a,个位数字是b的两位数是( )
| A. | ab | B. | a+10b | C. | ba | D. | 10a+b |
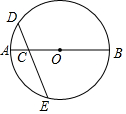 如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若$\widehat{AD}$的度数为35°,求$\widehat{BE}$的度数.
如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若$\widehat{AD}$的度数为35°,求$\widehat{BE}$的度数.