题目内容
9. 如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.(1)求一次函数与反比例函数的表达式;
(2)直线与y轴交于点C,连接OA、OC,计算△AOB的面积;
(3)根据图象直接写出:当x取何值时,反比例函数的值大于一次函数的值.
分析 (1)首先把A的坐标代入反比例函数解析式,求得反比例函数解析式,再求得B的坐标,利用待定系数法求得直线的解析式;
(2)首先求得C的坐标,然后根据S△AOB=S△OBC+S△AOC,利用三角形面积公式求解;
(3)根据函数图象确定反比例函数的值大于一次函数的值时x的范围,就是求反比例函数图象在上边时对应的自变量x的范围.
解答 解:(1)把A(2,3)代入y=$\frac{m}{x}$得m=6,则反比例函数的解析式是y=$\frac{6}{x}$;
把(-3,n)代入y=$\frac{6}{x}$得n=-2,则B的坐标是(-3,-2).
根据题意得:$\left\{\begin{array}{l}{2k+b=3}\\{-3k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
则直线的解析式是y=x+1;
(2)在y=x+1中,令x=0,解得y=1,
则C的坐标是(0,1).
则S△AOB=S△OBC+S△AOC=$\frac{1}{2}$×1×(2+3)=$\frac{5}{2}$;
(3)x的范围是x<-3或0小于0<x<1.
点评 用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
19.小明因流感在医院观察,要掌握他在一周内的体温是否稳定,则医生需了解小明7天体温的( )
| A. | 众数 | B. | 方差 | C. | 平均数 | D. | 频数 |
19.一个角的余角和这个角的补角也互为补角,这个角的度数等于( )
| A. | 90° | B. | 75° | C. | 45° | D. | 15° |
 将图中的△ABC作如下运动:
将图中的△ABC作如下运动: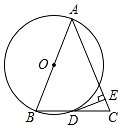 如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.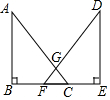 如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.
如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.