题目内容
18.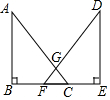 如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.
如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.
分析 要证明三角形ABC和DEF全等.这两个三角形中已知的条件有一组直角,AB=DE,那么只需证得BC=EF即可得出两三角形全等的结论,已知了BF=CE,等式两边都加上FC后,就可得出BC=EF,那么这两三角形也就全等了(SAS),根据全等三角形的性质得到∠ACB=∠DFE,再根据等腰三角形的性质即可求解.
解答 证明:∵AB⊥BE,DE⊥BE,
∴∠ABC=∠DEF=90°,
∵BF=CE,
∴BC=EF,
在△ABC与△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{∠ABC=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,
∴GC=GF.
点评 本题考查的是全等三角形的判定与性质.利用全等三角形来得出角相等或线段相等是解此类题的关键.

练习册系列答案
相关题目
7.对于有理数a、b,定义运算:a⊕b=a×b-a-b+1,则计算3⊕4的结果是( )
| A. | -12 | B. | 6 | C. | -6 | D. | 12 |
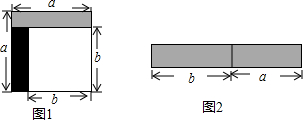 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2). 如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点. 如图,BE⊥CD于点E,CE=AE,BC=DA
如图,BE⊥CD于点E,CE=AE,BC=DA
 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.
每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,将△ABC绕点A逆时针旋转90°后得到△A′C′.