题目内容
2.有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下三个个结论中,(1)如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
(2)如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根;
(3)如果方程M和方程N有一个相同的根,那么这个根必是x=1;
错误的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 利用方程根的判别式和方程根的意义逐一分析判断即可.
解答 解:(1)如果方程M有两个不相等的实数根,则b2-4ac>0,方程N的判别式b2-4ac>0,有两个不相等的实数根,正确;
(2)如果5是方程M的一个根,则25a+5b+c=0,如果$\frac{1}{5}$是方程N的一个根,则$\frac{1}{25}$c+$\frac{1}{5}$b+a=0,即25a+5b+c=0,正确;
(3)a+c=0,当x=1或-1都成立,原题错误.
错误的个数是1.
故选:B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
10.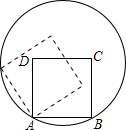 如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为( )
如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为( )
 如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为( )
如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为( )| A. | 2$\sqrt{2}$π | B. | ($\sqrt{2}$+1)π | C. | ($\sqrt{2}$+2)π | D. | ($\frac{2}{3}$$\sqrt{2}$+1)π |
12.已知关于x的一元二次方程ax2+bx+c=3的一根为x=2,且二次函数y=ax2+bx+c的对称轴是直线x=2,则抛物线的顶点坐标是( )
| A. | (2,3) | B. | (2,1) | C. | (2,-3) | D. | (3,2) |
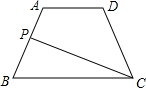 如图,在等腰梯形ABCD中,已知AD∥BC,AB=10,BC=15,tanB=$\frac{4}{3}$,点P是AB边上的一个动点.设BP=x,△BPC的面积为y,求y关于x的函数关系式,并写出x的取值范围.
如图,在等腰梯形ABCD中,已知AD∥BC,AB=10,BC=15,tanB=$\frac{4}{3}$,点P是AB边上的一个动点.设BP=x,△BPC的面积为y,求y关于x的函数关系式,并写出x的取值范围.