题目内容
10.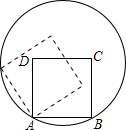 如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为( )
如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为( )| A. | 2$\sqrt{2}$π | B. | ($\sqrt{2}$+1)π | C. | ($\sqrt{2}$+2)π | D. | ($\frac{2}{3}$$\sqrt{2}$+1)π |
分析 作辅助线,首先求出∠D′AB的大小,进而求出旋转的角度,利用弧长公式问题即可解决.
解答 解:如图,分别连接OA、OB、OD′、OC、OC′;
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠OAB=60°;
同理可证:∠OAD′=60°,
∴∠D′AB=120°;
∵∠D′AB′=90°,
∴∠BAB′=120°-90°=30°,
由旋转变换的性质可知∠C′AC=∠B′AB=30°;
∵四边形ABCD为正方形,且边长为2,
∴∠ABC=90°,AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴当点D第一次落在圆上时,点C运动的路线长为:$\frac{30π×2\sqrt{2}}{180}$=$\frac{\sqrt{2}π}{3}$.
以D或B为圆心滚动时,每次C点运动$\frac{π}{3}$,
以A做圆心滚动两次,以B和D做圆心滚动三次,所以总路径=$\frac{\sqrt{2}π}{3}$×2+$\frac{π}{3}$×3=($\frac{2}{3}$$\sqrt{2}$+1)π.
故选:D.
点评 本题考查了正方形的性质、旋转的性质、等边三角形的判定和性质、勾股定理的运用以及弧长公式的运用,题目的综合性较强,解题的关键是正确的求出旋转角的度数.

练习册系列答案
相关题目
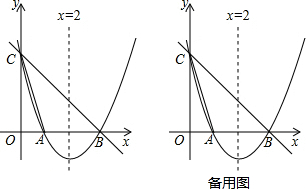
5. 已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x轴、y轴的交点分别为A、B,点P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0;②x=3是ax2+bx+3=0的一个根;③△PAB周长的最小值是$\sqrt{10}$+3$\sqrt{2}$.其中正确的是( )
已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x轴、y轴的交点分别为A、B,点P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0;②x=3是ax2+bx+3=0的一个根;③△PAB周长的最小值是$\sqrt{10}$+3$\sqrt{2}$.其中正确的是( )
 已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x轴、y轴的交点分别为A、B,点P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0;②x=3是ax2+bx+3=0的一个根;③△PAB周长的最小值是$\sqrt{10}$+3$\sqrt{2}$.其中正确的是( )
已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x轴、y轴的交点分别为A、B,点P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0;②x=3是ax2+bx+3=0的一个根;③△PAB周长的最小值是$\sqrt{10}$+3$\sqrt{2}$.其中正确的是( )| A. | 仅有①② | B. | 仅有②③ | C. | 仅有①③ | D. | ①②③ |
20.若α、β是方程x2+2x-2015=0的两个实数根,则α2+3α+β的值为( )
| A. | 2015 | B. | B、2013 | C. | -2015 | D. | 4030 |
 如图,D、E、F和A、B、C分别在同一直线上,若∠1=∠2,∠C=∠D,求证:∠A=∠F.
如图,D、E、F和A、B、C分别在同一直线上,若∠1=∠2,∠C=∠D,求证:∠A=∠F.