题目内容
17.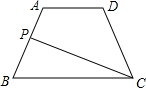 如图,在等腰梯形ABCD中,已知AD∥BC,AB=10,BC=15,tanB=$\frac{4}{3}$,点P是AB边上的一个动点.设BP=x,△BPC的面积为y,求y关于x的函数关系式,并写出x的取值范围.
如图,在等腰梯形ABCD中,已知AD∥BC,AB=10,BC=15,tanB=$\frac{4}{3}$,点P是AB边上的一个动点.设BP=x,△BPC的面积为y,求y关于x的函数关系式,并写出x的取值范围.
分析 过点P作PM⊥BC,交BC边于点M,由tanB=$\frac{4}{3}$,BP=x,设PM=4k,BM=3k,根据勾股定理列方程(4k)2+(3k)2=x2,求得PM=$\frac{4}{5}$x,然后根据三角形的面积公式即可得到结论.
解答  解:过点P作PM⊥BC,交BC边于点M,
解:过点P作PM⊥BC,交BC边于点M,
∴∠PMB=90°,
∴PM2+BM2=BP2,
∵tanB=$\frac{4}{3}$,BP=x,
设PM=4k,BM=3k,
∴(4k)2+(3k)2=x2,
∴k=$\frac{1}{5}$x,
∴PM=$\frac{4}{5}$x,
∵BC=15
∴y=$\frac{1}{2}$BC•PM,
即y=6x (0<x≤10).
点评 本题考查了等腰梯形的性质,勾股定理,三角函数,三角形的面积的计算,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
7.若x,y均为实数,且|x+1|+$\sqrt{y-1}$=0,则($\frac{x}{y}$)2015的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2015 |
9.下列两个变量之间,不存在函数关系的是( )
| A. | 一天的气温与时间之间的关系 | |
| B. | 一个正数的平方根与这个正数之间的关系 | |
| C. | 圆的面积与圆的周长之间的关系 | |
| D. | 速度一定,汽车行驶的路程与行驶时间之间的关系 |
 如图,已知有理数a,b对应数轴上两点A,B.为让算式-12-|a□b|计算出来的值最大,算式中的□所在位置应选择的运算符号是( )
如图,已知有理数a,b对应数轴上两点A,B.为让算式-12-|a□b|计算出来的值最大,算式中的□所在位置应选择的运算符号是( ) 如图,D、E、F和A、B、C分别在同一直线上,若∠1=∠2,∠C=∠D,求证:∠A=∠F.
如图,D、E、F和A、B、C分别在同一直线上,若∠1=∠2,∠C=∠D,求证:∠A=∠F.