题目内容
18.已知x2-3x-1=0,且x<0,求代数式(1)x+$\frac{1}{x}$;(2)x2+$\frac{1}{{x}^{2}}$的值.分析 已知等式两边除以x,表示求出x-$\frac{1}{x}$=3,两边平方并利用完全平方公式化简求出x2+$\frac{1}{{x}^{2}}$的值,再利用完全平方公式求出x+$\frac{1}{x}$的值即可.
解答 解:已知等式x2-3x-1=0,且x<0,
两边除以x得:x-$\frac{1}{x}$=3,
两边平方得:(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2=9,即x2+$\frac{1}{{x}^{2}}$=11,
则(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2=13,即x+$\frac{1}{x}$=-$\sqrt{13}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
10.下列各式中运算正确的式子是( )
| A. | a3•a2=a6 | B. | (-a3)2=a5 | C. | $-\sqrt{{{({-3})}^2}}=-3$ | D. | ${(-1)^{-2}}=\frac{1}{2}$ |
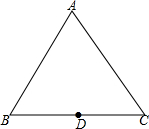 如图,三角形ABC是边长为2的等边三角形,D为BC的中点,请在AC上找一点E,使得BE+ED的和最小,并求出这个最小值.
如图,三角形ABC是边长为2的等边三角形,D为BC的中点,请在AC上找一点E,使得BE+ED的和最小,并求出这个最小值.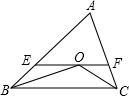 已知:如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于F.求∠BOC的度数.
已知:如图,∠ABC=50°,∠ACB=60°,∠ABC、∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于F.求∠BOC的度数.