题目内容
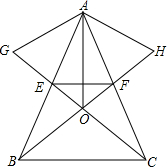 如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证:
如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证:(1)BH=CG;
(2)AO平分∠BAC.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)根据已知条件结合图形可以判断△AGC≌△AHB,利用全等三角形的性质即可证明BH=CG;
(2)观察图形容易发现,欲证明AO平分∠BAC,只要证明△ABO≌△ACO,为此只需证明OB=OC,∠ABO=∠ACO.
(2)观察图形容易发现,欲证明AO平分∠BAC,只要证明△ABO≌△ACO,为此只需证明OB=OC,∠ABO=∠ACO.
解答:解:(1)∵△AEG和△AFH均为等边三角形,
∴∠GAE=∠HAF=60°,AG=AE,AH=AF;
∵∠GAC=∠GAE+∠EAC,∠HAB=∠HAF+∠FAB,
∴∠GAC=∠HAB;
∵EF∥BC,
∴
=
,而AB=AC,
∴AE=AF.
又∵AG=AE,AH=AF,
∴AG=AH;
在△AGC与△AHB中,
,
∴△AGC≌△AHB(SAS),
∴BH=CG.
 (2)∵AB=AC,AE=AF,
(2)∵AB=AC,AE=AF,
∴BE=CF;
又∵EF∥BC,
∴四边形BCFE为等腰梯形,
故∠EBC=∠FCB,EC=FB;
在△EBC与△FCB中,
,
∴△EBC≌△FCB(SSS),
∴∠OCB=∠OBC,故OB=OC;
又∵∠ABC=∠ACB,
∴∠ABO=∠ACO;
在△ABO与△ACO中,
,
∴△ABO≌△ACO(SAS),
∴∠BAO=∠CAO,
即AO平分∠BAC.
∴∠GAE=∠HAF=60°,AG=AE,AH=AF;
∵∠GAC=∠GAE+∠EAC,∠HAB=∠HAF+∠FAB,
∴∠GAC=∠HAB;
∵EF∥BC,
∴
| AE |
| AB |
| AF |
| AC |
∴AE=AF.
又∵AG=AE,AH=AF,
∴AG=AH;
在△AGC与△AHB中,
|
∴△AGC≌△AHB(SAS),
∴BH=CG.
 (2)∵AB=AC,AE=AF,
(2)∵AB=AC,AE=AF,∴BE=CF;
又∵EF∥BC,
∴四边形BCFE为等腰梯形,
故∠EBC=∠FCB,EC=FB;
在△EBC与△FCB中,
|
∴△EBC≌△FCB(SSS),
∴∠OCB=∠OBC,故OB=OC;
又∵∠ABC=∠ACB,
∴∠ABO=∠ACO;
在△ABO与△ACO中,
|
∴△ABO≌△ACO(SAS),
∴∠BAO=∠CAO,
即AO平分∠BAC.
点评:考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知方程(m-2)x|m|-1+3=5是关于x的一元一次方程,则m的值是( )
| A、+2 | B、2 |
| C、-2 | D、无法确定 |
下列说法正确的是( )
| A、为了解全市中学生的睡眠状况,宜采用普查方式 |
| B、某地会发生地震是必然事件 |
| C、某校教师150人,其中31岁~35岁组的频率为0.2,那么在该段的教师有30人 |
| D、若甲组数据的方差S甲2=0.1,乙组数据的方差S乙2=0.2,则乙组数据比甲组稳定 |
 如图,在平行四边形ABCD中,∠ABC的平分线BE与AD交于点E,且ED=2AE,AE=3,则平行四边形ABCD的周长是
如图,在平行四边形ABCD中,∠ABC的平分线BE与AD交于点E,且ED=2AE,AE=3,则平行四边形ABCD的周长是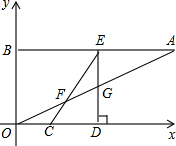 如图,在平面直角坐标系xOy中,点A、B的坐标分别为(16,8)、(0,8),线段CD在x轴上,CD=6,点C从原点出发沿x轴正方向以每秒2个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
如图,在平面直角坐标系xOy中,点A、B的坐标分别为(16,8)、(0,8),线段CD在x轴上,CD=6,点C从原点出发沿x轴正方向以每秒2个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E,交OA于点G,连接CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.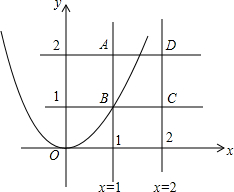 在平面直角坐标系中,有四条直线x=1,x=2,y=1,y=2围成的正方形ABCD(如图所示).
在平面直角坐标系中,有四条直线x=1,x=2,y=1,y=2围成的正方形ABCD(如图所示). 如图,在△ABC中,点D在BC上,BD=AD=AC,∠BAC=60°,求∠B的度数.
如图,在△ABC中,点D在BC上,BD=AD=AC,∠BAC=60°,求∠B的度数.