题目内容
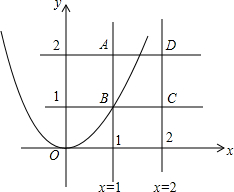 在平面直角坐标系中,有四条直线x=1,x=2,y=1,y=2围成的正方形ABCD(如图所示).
在平面直角坐标系中,有四条直线x=1,x=2,y=1,y=2围成的正方形ABCD(如图所示).(1)若一条抛物线y=ax2与正方形ABCD有公共点,求该抛物线的二次项系数a的取值范围;
(2)如果抛物线与正方形ABCD没有公共点,求a的取值范围.
考点:二次函数综合题
专题:
分析:(1)根据抛物线经过A点时,可得抛物线中a的值最大,抛物线经过C点时,可得抛物线中a的值最小;
(2)根据抛物线与正方形没有公共点,可得抛物线中a值大于抛物线经过A点时a的值,抛物线中a值小于抛物线经过点C时a的值.
(2)根据抛物线与正方形没有公共点,可得抛物线中a值大于抛物线经过A点时a的值,抛物线中a值小于抛物线经过点C时a的值.
解答:解:(1)由|a|越大,抛物线开口越小,得
抛物线经过A点时,抛物线的a值最大,2=a×12,
解得a=2;
经过C点时,可得抛物线y=ax2与正方形ABCD有公共点时a的最小值,
即22a=1,解得a=
,
综上所述:
≤a≤2时,一条抛物线y=ax2与正方形ABCD有公共点;
(2)由(1)得,当a>2或0<a<
时,开口向上的抛物线与正方形ABCD没有公共点;
当a<0时,p抛物线开口向下,抛物线与正方形ABCD没有公共点,
综上所述:当a<0,0<a<
,a>2时,抛物线与正方形ABCD没有公共点.
抛物线经过A点时,抛物线的a值最大,2=a×12,
解得a=2;
经过C点时,可得抛物线y=ax2与正方形ABCD有公共点时a的最小值,
即22a=1,解得a=
| 1 |
| 4 |
综上所述:
| 1 |
| 4 |
(2)由(1)得,当a>2或0<a<
| 1 |
| 4 |
当a<0时,p抛物线开口向下,抛物线与正方形ABCD没有公共点,
综上所述:当a<0,0<a<
| 1 |
| 4 |
点评:本题考查了二次函数综合题,利用了二次函数的性质:|a|越大,抛物线开口越小.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
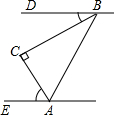 如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )
如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )| A、20° | B、40° |
| C、50° | D、70° |
已知|a+13|+|b-10|=0,则a+b的值是( )
| A、-3 | B、3 | C、23 | D、-23 |
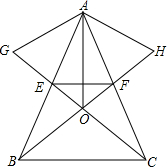 如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证:
如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证:(1)BH=CG;
(2)AO平分∠BAC.
下列四个数中最小的数是( )
| A、5 | ||
B、-
| ||
| C、0 | ||
| D、-2 |
 抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.
抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.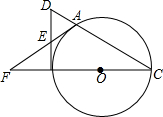 如图,A是以BC为直径的⊙O上一点,过点B作圆O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.
如图,A是以BC为直径的⊙O上一点,过点B作圆O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F. 以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为
以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为