题目内容
请阅读下列材料:
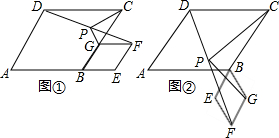
问题:如图①,将菱形ABCD和菱形BEFG拼接在一起,使得点A,B,E在同一条直线上,点G在BC边上,P是线段DF的中点,连接PG,PC.若∠ABC=120°,试探究PG与PC的位置关系及∠PCG的大小.小明同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.请你参考小明的思路,探究并解决下列问题:
(1)直接写出上面问题中线段PG与PC的位置关系及∠PCG的大小;
(2)将图①中的菱形BEFG绕点B顺时针旋转,使点E恰好落在CB的延长线上,原问题中的其他条件不变(如图②).你在(1)中得到的两个结论是否仍成立?写出你的猜想并加以证明.
问题:如图①,将菱形ABCD和菱形BEFG拼接在一起,使得点A,B,E在同一条直线上,点G在BC边上,P是线段DF的中点,连接PG,PC.若∠ABC=120°,试探究PG与PC的位置关系及∠PCG的大小.小明同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.请你参考小明的思路,探究并解决下列问题:
(1)直接写出上面问题中线段PG与PC的位置关系及∠PCG的大小;
(2)将图①中的菱形BEFG绕点B顺时针旋转,使点E恰好落在CB的延长线上,原问题中的其他条件不变(如图②).你在(1)中得到的两个结论是否仍成立?写出你的猜想并加以证明.

考点:菱形的性质,全等三角形的判定与性质
专题:
分析:(1)延长GP交DC于点H,构造全等三角形,从而得出DH=GF,PH=PG,进而得出△GCH是等腰三角形,得出PG⊥PC,∠PCG=∠PCH,由∠ABC=120°,得出∠BCD=60°,即可证得∠PCG=30°;
(2)延长GP交AD于点H,先证得△DPH≌△FPG,从而得出PH=PG,DH=FG=BG,进进而证得△CDH≌△CBG,得出CH=CG,∠DCH=∠BCG,即可证得CP⊥PG,由∠HCG=∠HCB+∠BCG=∠HCB+∠DCH=∠DCB=60°,证得∠PCG=
∠HCG=30°.
(2)延长GP交AD于点H,先证得△DPH≌△FPG,从而得出PH=PG,DH=FG=BG,进进而证得△CDH≌△CBG,得出CH=CG,∠DCH=∠BCG,即可证得CP⊥PG,由∠HCG=∠HCB+∠BCG=∠HCB+∠DCH=∠DCB=60°,证得∠PCG=
| 1 |
| 2 |
解答: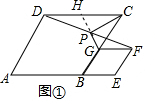 解:(1)PG⊥PC,∠PCG=30°;
解:(1)PG⊥PC,∠PCG=30°;
如图①,延长GP交DC于点H,
∵在菱形ABCD和菱形BEFG中,AE∥DC,AE∥GF,
∴DC∥GF,
∴∠PDH=∠PFG,
在△PDH和△PFG中,
,
∴△PDH≌△PFG(ASA),
∴DH=GF,PH=PG,
∵BG=GF,
∴DH=BG,
∵DC=BC,
∴HC=GC,
∴△GCH是等腰三角形,
∴PG⊥PC,∠PCG=∠PCH,
∵∠ABC=120°,
∴∠BCD=60°,
∴∠PCG=30°;
(2)(1)中两个结论仍成立;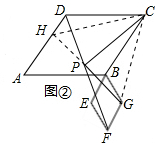
证明:如图②,延长GP交AD于点H,连接CG,
∵四边形ABCD和BEFG是菱形
∴AD∥BC,BE∥FG,
∵E在CB的延长线上
∴AD∥FG,
∴∠HDP=∠GFP,
在△DPH和△FPG中,
,
∴△DPH≌△FPG(ASA),
∴PH=PG,DH=FG=BG,
在△CDH和△CBG中,
,
∴△CDH≌△CBG(SAS),
∴CH=CG,∠DCH=∠BCG,
∴CP⊥PG,
∵∠HCG=∠HCB+∠BCG=∠HCB+∠DCH=∠DCB=60°,
∴∠PCG=
∠HCG=30°.
 解:(1)PG⊥PC,∠PCG=30°;
解:(1)PG⊥PC,∠PCG=30°;如图①,延长GP交DC于点H,
∵在菱形ABCD和菱形BEFG中,AE∥DC,AE∥GF,
∴DC∥GF,
∴∠PDH=∠PFG,
在△PDH和△PFG中,
|
∴△PDH≌△PFG(ASA),
∴DH=GF,PH=PG,
∵BG=GF,
∴DH=BG,
∵DC=BC,
∴HC=GC,
∴△GCH是等腰三角形,
∴PG⊥PC,∠PCG=∠PCH,
∵∠ABC=120°,
∴∠BCD=60°,
∴∠PCG=30°;
(2)(1)中两个结论仍成立;

证明:如图②,延长GP交AD于点H,连接CG,
∵四边形ABCD和BEFG是菱形
∴AD∥BC,BE∥FG,
∵E在CB的延长线上
∴AD∥FG,
∴∠HDP=∠GFP,
在△DPH和△FPG中,
|
∴△DPH≌△FPG(ASA),
∴PH=PG,DH=FG=BG,
在△CDH和△CBG中,
|
∴△CDH≌△CBG(SAS),
∴CH=CG,∠DCH=∠BCG,
∴CP⊥PG,
∵∠HCG=∠HCB+∠BCG=∠HCB+∠DCH=∠DCB=60°,
∴∠PCG=
| 1 |
| 2 |
点评:本题考查了菱形的性质,三角形全等的判定和性质,等腰三角形的性质等,作出辅助线构建全等三角形是本题的关键.

练习册系列答案
相关题目
已知|a+13|+|b-10|=0,则a+b的值是( )
| A、-3 | B、3 | C、23 | D、-23 |
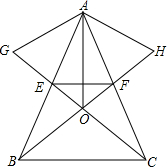 如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证:
如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证: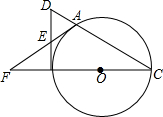 如图,A是以BC为直径的⊙O上一点,过点B作圆O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.
如图,A是以BC为直径的⊙O上一点,过点B作圆O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F. 以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为
以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为 如图,在△ABC中,AD是BC边上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F.若△ABC的面积为3,则四边形EFDC的面积为
如图,在△ABC中,AD是BC边上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F.若△ABC的面积为3,则四边形EFDC的面积为