题目内容
 如图,在平行四边形ABCD中,∠ABC的平分线BE与AD交于点E,且ED=2AE,AE=3,则平行四边形ABCD的周长是
如图,在平行四边形ABCD中,∠ABC的平分线BE与AD交于点E,且ED=2AE,AE=3,则平行四边形ABCD的周长是考点:平行四边形的性质
专题:
分析:由?ABCD,根据平行四边形的对边平行且相等,可得AD∥BC,AD=BC,AB=CD,又由BE是∠ABC的平分线,可得∠ABE=∠CBE,易得AE=AB(等角对等边),即可求得?ABCD的周长.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∵AE:ED=1:2,
∴ED=6,
∴AD=AE+ED=9,
∴?ABCD的周长是24.
故答案为:24.
∴AD∥BC,AD=BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=3,
∵AE:ED=1:2,
∴ED=6,
∴AD=AE+ED=9,
∴?ABCD的周长是24.
故答案为:24.
点评:本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果汽车向东行驶3公里记作3公里,向西2公里应记作( )
| A、+2公里 | B、-2公里 |
| C、+3公里 | D、-3公里 |
已知|a+13|+|b-10|=0,则a+b的值是( )
| A、-3 | B、3 | C、23 | D、-23 |
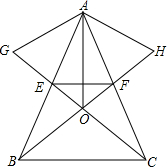 如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证:
如图,在△ABC中,AB=AC,EF∥BC交AB于点E,交AC于点F,分别以AE、AF为边在△ABC的外部作等边△AEG和△AFH,BF、CG交于点O.求证: 如图,在△ABC中,AD是BC边上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F.若△ABC的面积为3,则四边形EFDC的面积为
如图,在△ABC中,AD是BC边上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F.若△ABC的面积为3,则四边形EFDC的面积为