题目内容
3.阅读下列材料,解答问题:∵2<$\sqrt{7}$<3,∴$\sqrt{7}$的整数部分为2,小数部分为$\sqrt{7}$-2.
请你观察上述的规律后试解下面的问题:
如果$\sqrt{12}$的小数部分为a,$\sqrt{12}$的小数部分为b.
求:a=3,b=$\sqrt{12}$-3,和ab-b2的值.
分析 根据题意确定出a与b的值,代入原式计算即可得到结果.
解答 解:∵3<$\sqrt{12}$<4,∴$\sqrt{12}$的整数部分为3,小数部分为$\sqrt{12}$-3.
∴a=3,b=$\sqrt{12}$-3,
故答案为:3,$\sqrt{12}$-3;
ab-b2 =b(a-b)=($\sqrt{12}$-3)(6-$\sqrt{12}$)=-18+18$\sqrt{3}$.
点评 本题主要考查了估算无理数的大小,利用夹逼法是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
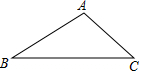 已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.
已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.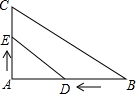 在Rt△ABC中,A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间,△ADE与△ABC相似?
在Rt△ABC中,A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间,△ADE与△ABC相似?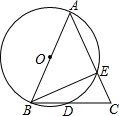 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E