题目内容
13.角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,三条角平分线的交点O到三边的距离为r.连接OA、OB、OC,△ABC被划分为三个小三角形.∵S=S△OBC+S△OAC+S△OAB=$\frac{1}{2}$BC•r+$\frac{1}{2}$AC•r+$\frac{1}{2}$AB•r=$\frac{1}{2}$(a+b+c)•r,∴r=$\frac{2S}{a+b+c}$
(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求点O到四边的距离r;
(2)理解应用:如图(3),在四边形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,对角线BD=20,点O1与O2分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为r1和r2,求$\frac{{r}_{1}}{{r}_{2}}$的值.
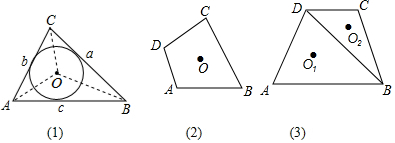
分析 (1)已知已给出示例,我们仿照例子,连接OA,OB,OC,OD,则四边形被分为四个小三角形,且每个三角形都以内切圆半径为高,以四边形各边作底,这与题目情形类似.仿照证明过程,r易得;
(2)(1)中已告诉我们内切圆半径的求法,如是我们再相比即得结果.但求内切圆半径需首先知道三角形各边边长,根据等腰梯形性质,过点D作AB垂线,进一步易得BD的长,则r1、r2、$\frac{{r}_{1}}{{r}_{2}}$易得.
解答  解:(1)如图,连接OA、OB、OC、OD,
解:(1)如图,连接OA、OB、OC、OD,
∵S=S△AOB+S△BOC+S△COD+S△AOD=$\frac{1}{2}$ar+$\frac{1}{2}$br+$\frac{1}{2}$cr+$\frac{1}{2}$dr=$\frac{1}{2}$(a+b+c)r,
∴r=$\frac{2S}{a+b+c+d}$;
(2)∵AB∥CD,
∴S△ABD:S△BCD=AB:CD=21:11;
∵r1=$\frac{2{S}_{△ABD}}{AB+BD+AD}$=$\frac{2{S}_{△ABD}}{54}$,
r2=$\frac{2{S}_{△CDB}}{CD+CB+DB}$=$\frac{2{S}_{△CDB}}{44}$,
∴$\frac{{r}_{1}}{{r}_{2}}$=$\frac{{S}_{△ABD}}{27}$:$\frac{{S}_{△BCD}}{22}$=$\frac{{S}_{△ABD}}{27}$×$\frac{22}{{S}_{△BCD}}$=$\frac{21×22}{27×11}$=$\frac{14}{9}$.
点评 本题考查了角平分线的定义,三角形面积计算以及等腰梯形等相关知识的综合应用,这类创新性题目已经成为新课标热衷的考点,同时要求学生在日常的学习中要注重自我学习能力的培养.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案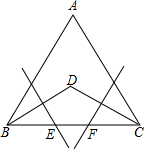 如图,△ABC是正三角形,∠B和∠C的平分线相交于D,BD,CD的垂直平分线分别交BC于E,F.求证:BE=CF.
如图,△ABC是正三角形,∠B和∠C的平分线相交于D,BD,CD的垂直平分线分别交BC于E,F.求证:BE=CF. 如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(2,2)处,两直角边分别与坐标轴交于点A、B,则OA+OB的值为4.
如图,在平面直角坐标系中,将直角三角形的直角顶点放在点P(2,2)处,两直角边分别与坐标轴交于点A、B,则OA+OB的值为4.