题目内容
11．
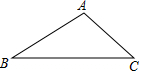已知：如图，在△ABC中，∠B=30°，∠C=45°，AC=2$\sqrt{2}$．（1）AB的长为2；
（2）S△ABC=2+2$\sqrt{3}$．
分析 过点A作AD⊥BC于D，根据锐角三角函数的定义求出AD的长，再根据锐角三角函数的定义求出AB的长，进而利用三角形面积公式解答即可．
解答 解：（1）过点A作AD⊥BC于D，
∵AD⊥BC，
∴∠ADC=90°．
在Rt△ADC中，
∵∠C=45°，AC=2$\sqrt{2}$．
∴AD=DC=2，
在Rt△ABD中，
∵∠B=30°，AD=2，
∴AB=4；
（2）S△ABC=$\frac{1}{2}×2×（2+2\sqrt{3}）=2+2\sqrt{3}$，
故答案为：2；2+2$\sqrt{3}$
点评 本题考查的是解直角三角形，熟记锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
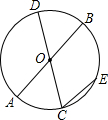如图，AB、CD是⊙O的直径，弦CE∥AB，$\widehat{AC}$的度数为70°．求∠EOC的度数．
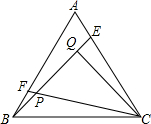如图所示，点E、F分别是正△ABC的边AC、AB上的点，AE=BF，BE，CF相交于点P，CQ⊥BE于Q，若PF=1，PQ=3，则BE=7．