题目内容
18.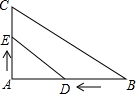 在Rt△ABC中,A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间,△ADE与△ABC相似?
在Rt△ABC中,A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间,△ADE与△ABC相似?
分析 根据相似三角形的对应边成比例可得出$\frac{AE}{AC}$=$\frac{AD}{AB}$或$\frac{AE}{AB}$=$\frac{AD}{AC}$,设运动的时间是t秒,则AE=t,AD=8-2t,代入比例式求出t的值即可.
解答 解:∵△ADE 与△ABC相似,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$或$\frac{AE}{AB}$=$\frac{AD}{AC}$.
设运动的时间是t秒,
则AE=t,AD=8-2t
∴$\frac{t}{6}$=$\frac{8-2t}{8}$或$\frac{8-2t}{6}$=$\frac{t}{8}$,解得t=$\frac{12}{5}$或$\frac{32}{11}$.
∴经过t=12/5或32/11秒两个三角形相似.
点评 本题考查的是相似三角形的判定,在解答此题时要注意分两种情况进行讨论,不要漏解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.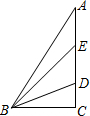 如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
 如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
如图,在△ABC中∠C=90°,D、E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )| A. | BE是△ABD的中线 | B. | BD是△BCE的角平分线 | ||
| C. | ∠ABE=∠EBD=∠DBC | D. | BC是△ABE的高 |
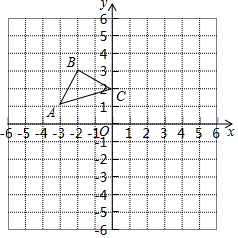 如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么位置关系,请说明理由.
如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC有什么位置关系,请说明理由.