题目内容
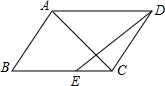 已知如图,平行四边形ABCD中,CE:BE=1:3,且S△EFC=1,那么S△ABC=
已知如图,平行四边形ABCD中,CE:BE=1:3,且S△EFC=1,那么S△ABC=考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:易证△AFD∽△CFE,利用相似的性质可求出△AFD的面积,再根据高相等的三角形面积之比等于底之比可求出△DFC的面积,进而可求出△ACD的面积,又因为△ABC的面积等于△ADC的面积,问题得解.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△AFD∽△CFE,
∵CE:BE=1:3,
∴CE:BC=CE:AD=1:4,
∴S△AFD:S△CFE=1:16,
∵S△EFC=1,
∴S△AFD=16,
∵EF:FD=1:4,
∴S△EFC:S△DFC=1:4,
∴S△ABC=S△ADC=4+16=20,
故答案为:20.
∴AD∥BC,AD=BC,
∴△AFD∽△CFE,
∵CE:BE=1:3,
∴CE:BC=CE:AD=1:4,
∴S△AFD:S△CFE=1:16,
∵S△EFC=1,
∴S△AFD=16,
∵EF:FD=1:4,
∴S△EFC:S△DFC=1:4,
∴S△ABC=S△ADC=4+16=20,
故答案为:20.
点评:本题考查了平行四边形的性质、相似三角形的判定和性质,解题的关键是熟知高相等的三角形面积之比等于底之比.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
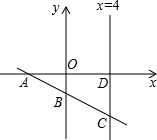 如图,在直角坐标系内,一次函数y=kx+b(kb>0,b<0)的图象分别与x轴、y轴和直线x=4相交于A、B、C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是10.若点A的横坐标是-
如图,在直角坐标系内,一次函数y=kx+b(kb>0,b<0)的图象分别与x轴、y轴和直线x=4相交于A、B、C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是10.若点A的横坐标是-