题目内容
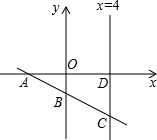 如图,在直角坐标系内,一次函数y=kx+b(kb>0,b<0)的图象分别与x轴、y轴和直线x=4相交于A、B、C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是10.若点A的横坐标是-
如图,在直角坐标系内,一次函数y=kx+b(kb>0,b<0)的图象分别与x轴、y轴和直线x=4相交于A、B、C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是10.若点A的横坐标是-| 1 |
| 2 |
考点:待定系数法求一次函数解析式
专题:计算题
分析:由题意确定出A的坐标,代入一次函数解析式得到关于k与b的方程,表示出B与C的坐标,利用梯形面积公式表示出四边形OBCD面积,将已知面积代入得到关于k与b的方程,联立求出k与b的值,即可确定出一次函数解析式.
解答:解:由A的横坐标为-
,得到A(-
,0),
把A坐标代入一次函数y=kx+b解析式得:-
k+b=0①,
令x=0,得到y=b,即B(0,b),
令x=4,得到y=4k+b,即C(4,4k+b),
∵S四边形OBCD=
(OB+CD)•OD=10,即
×(-b-4k-b)×4=10,
∴4k+2b=-5②,
联立①②,解得:k=-1,b=-
,
则一次函数解析式为y=-x-
.
| 1 |
| 2 |
| 1 |
| 2 |
把A坐标代入一次函数y=kx+b解析式得:-
| 1 |
| 2 |
令x=0,得到y=b,即B(0,b),
令x=4,得到y=4k+b,即C(4,4k+b),
∵S四边形OBCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴4k+2b=-5②,
联立①②,解得:k=-1,b=-
| 1 |
| 2 |
则一次函数解析式为y=-x-
| 1 |
| 2 |
点评:此题考查了待定系数法求一次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个数增加2倍再加上22,和为55,这个数是( )
| A、22 | B、33 | C、11 | D、44 |
计算(-x2)3的结果是( )
| A、-x5 |
| B、-x6 |
| C、x5 |
| D、x6 |
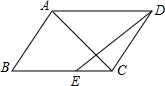 已知如图,平行四边形ABCD中,CE:BE=1:3,且S△EFC=1,那么S△ABC=
已知如图,平行四边形ABCD中,CE:BE=1:3,且S△EFC=1,那么S△ABC= 如图,某校计划在边长为a米的正方形场地上,修建两条宽为x(x<a)米的通道,其余部分进行绿化.
如图,某校计划在边长为a米的正方形场地上,修建两条宽为x(x<a)米的通道,其余部分进行绿化. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为
如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为