题目内容
第1个△ABC的面积为1,它的三条中位线组成第2个三角形,第2个三角形三条中位线组成第3个三角形,照上述方法继续做下去,则第n个三角形的面积为 .
考点:三角形中位线定理
专题:规律型
分析:由A2,B2,C2分别是△A1B1C1各边的中点,根据三角形中位线的性质和有三组对应边的比相等的两个三角形相似得到△A2B2C2∽△A1B1C1,所以S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,得到即S△A2B2C2=
,同理可得S△A3B3C3=
×
=(
)2,以此类推即可得到第n个三角形的面积.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答: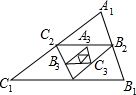 解:∵A2,B2,C2分别是△A1B1C1各边的中点,
解:∵A2,B2,C2分别是△A1B1C1各边的中点,
∴△A2B2C2∽△A1B1C1,
∴S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,
即S△A2B2C2=
,
∴S△A3B3C3=
×
=(
)2,
以此类推…
∴第n个三角形的面积是(
)n-1=(
)2n-2,
故答案为:(
)2n-2.
 解:∵A2,B2,C2分别是△A1B1C1各边的中点,
解:∵A2,B2,C2分别是△A1B1C1各边的中点,∴△A2B2C2∽△A1B1C1,
∴S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,
即S△A2B2C2=
| 1 |
| 4 |
∴S△A3B3C3=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
以此类推…
∴第n个三角形的面积是(
| 1 |
| 4 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查了三角形中位线定理以及三角形相似的判定与性质,解题的关键是找到问题的一般规律.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
计算(-x2)3的结果是( )
| A、-x5 |
| B、-x6 |
| C、x5 |
| D、x6 |
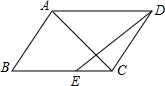 已知如图,平行四边形ABCD中,CE:BE=1:3,且S△EFC=1,那么S△ABC=
已知如图,平行四边形ABCD中,CE:BE=1:3,且S△EFC=1,那么S△ABC= 如图,AC,BC的中垂线交于P点,则PA
如图,AC,BC的中垂线交于P点,则PA 如图∠DBC=∠BCE=90°,M为DE中点.求证:MB=MC.
如图∠DBC=∠BCE=90°,M为DE中点.求证:MB=MC. 如图,四棱柱的高为6米,底面是边长为4米的正方形,一只小甲壳虫从如图的顶点A开始,爬向顶点B.那么它爬行的最短路程为
如图,四棱柱的高为6米,底面是边长为4米的正方形,一只小甲壳虫从如图的顶点A开始,爬向顶点B.那么它爬行的最短路程为