题目内容
3.如图,已知⊙O的半径为1,线段AB=4,⊙O从A端开始沿着线段滚向B端,设⊙O与AB切于点P,当P与A、B不重合时,分别过A,B两点作与⊙O相切(切点为E,F),但不与AB重合的两条射线.问:(1)当∠EAB=90°时,AP有多长?(直接写出答案)
(2)当AE与BF相交于点C且∠ACB=60°,求△ABC的周长;
(3)当AE∥BF时,求AP的长.

分析 (1)如图1,连接OP,OE,由AB,AE与⊙O相切,得到∠OEA=∠OPA=90°,推出四边形APOE是正方形,根据正方形的性质得到AP=OE=1;
(2)如图2,连接EF,则CE=CF,由∠ACB=60°,得到△CEF是等腰三角形,连接OE,OF.过O作OG⊥EF于G,由∠CEO=∠CFO=90°,得到∠EOF=120°,于是得到∠OFE=∠OEF=30°,根据直角三角形的性质即可得到结论$\sqrt{3}$;
(3)如图(3)连接OE,OF,于是得到OE⊥AE,OF⊥BF,根据平行线的性质得到点E,O,F共线,过B作BH⊥AE,得到BH=EF=2,根据勾股定理得到AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=2$\sqrt{3}$,设BF=EH=x,即可得到结论.
解答  解:(1)如图1,连接OP,OE,
解:(1)如图1,连接OP,OE,
∵AB,AE与⊙O相切,
∴∠OEA=∠OPA=90°,
∵∠EAP=90°,OE=OP,
∴四边形APOE是正方形,
∴AP=OE=1;
(2)如图2,连接EF,则CE=CF,
∵∠ACB=60°,
∴△CEF是等腰三角形,
连接OE,OF.过O作OG⊥EF于G,
∵∠CEO=∠CFO=90°,
∴∠EOF=120°,
∴∠OFE=∠OEF=30°,
∴OG=$\frac{1}{2}$,EG =$\frac{\sqrt{3}}{2}$,
=$\frac{\sqrt{3}}{2}$,
∴$EF=2EG=\sqrt{3}$,
∴CE=CF=$\sqrt{3}$,
∵AP=AE,PB=BF,
∴AE+BF=AB=4,
∴△ABC的周长=4+4+2$\sqrt{3}$=8+2$\sqrt{3}$;
(3)如图(3)连接OE,OF,则OE⊥AE,OF⊥BF,
∵AE∥BF,
∴OE⊥BF,
∴点E,O,F共线,
过B作BH⊥AE,
∴BH=EF=2,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=2$\sqrt{3}$,
设BF=EH=x,则AP=AE=2$\sqrt{3}$+x,BP=BF=x,
∴2$\sqrt{3}$+x+x=4,
∴x=2-$\sqrt{3}$,
∴AP=4-(2-$\sqrt{3}$)=2+$\sqrt{3}$.
点评 本题考查了切线的性质,勾股定理,平行线的性质,等腰三角形的判定,正确的作出辅助线是解题的关键.

 如图,直线AB和CD相交于点O,OE⊥AB,∠AOC=30°,则∠DOE的度数是( )
如图,直线AB和CD相交于点O,OE⊥AB,∠AOC=30°,则∠DOE的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.
如图,在平面直角坐标系中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°. 如图,半径为1的⊙P的圆心在抛物线y=-x2+4x-3上运动,当⊙P在x轴相切时,圆心P的坐标是(2,1),(2+$\sqrt{2}$,-1),(2-$\sqrt{2}$,-1).
如图,半径为1的⊙P的圆心在抛物线y=-x2+4x-3上运动,当⊙P在x轴相切时,圆心P的坐标是(2,1),(2+$\sqrt{2}$,-1),(2-$\sqrt{2}$,-1).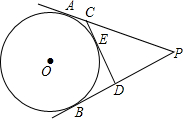 如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是12.
如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是12. 如图,△EDC是由△EAB绕点E顺时针旋转40°后得到的图形,则∠BFD的度数是40°.
如图,△EDC是由△EAB绕点E顺时针旋转40°后得到的图形,则∠BFD的度数是40°.