题目内容
5．若（a+$\sqrt{2}$）2与|b-1|互为相反数，则2b-a的值为（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$+2 | C． | $\sqrt{2}$-2 | D． | 2-$\sqrt{2}$ |
分析 直接利用偶次方的性质以及绝对值的性质得出a，b的值，进而求出答案．
解答 解：∵（a+$\sqrt{2}$）2与|b-1|互为相反数，
∴a+$\sqrt{2}$=0，b-1=0，
解得：a=-$\sqrt{2}$，b=1，
则2b-a的值为：2×1+$\sqrt{2}$=2+$\sqrt{2}$．
故选：B．
点评 此题主要考查了偶次方的性质以及绝对值的性质，正确得出a，b的值是解题关键．
练习册系列答案
相关题目
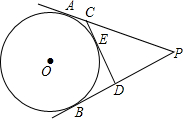如图，PA、PB切⊙O于点A、B，PA=6，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长是12．
如图，在一张面积为48cm2的正方形硬纸板的四周各剪去一个同样大小的面积为3cm2的小正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计），那么这个长方体盒子的体积是多少？