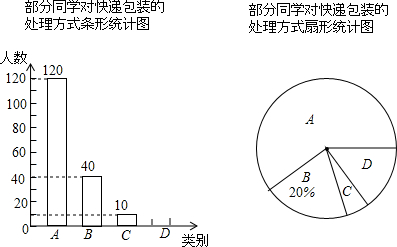
题目内容
16.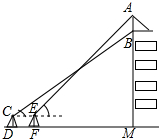 为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.
为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示).小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75.
分析 过点C作CN⊥AM于点N,则点C,E,N在同一直线上,设AB=x米,在Rt△AEN中表示出EN的长度,Rt△BCN中,根据三角函数的知识,代入求出x的值,即可得解.
解答 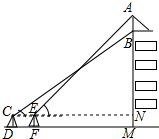 解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
设AB=x米,则AN=x+(19-1)=x+18(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+18,
在Rt△BCN中,∠BCN=37°,BM=19m,
∴tan∠BCN=$\frac{BN}{CN}$=0.75,
∴$\frac{18}{x+18+4.8}$=$\frac{3}{4}$,
解得:x=1.2.
经检验:x=1.2是原分式方程的解.
答:宣传牌AB的高度约为1.2m.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
11.若关于x一元二次方程x2-10x+k+1=0有两个相等的实数根,则k的值为( )
| A. | 8 | B. | 9 | C. | 12 | D. | 24 |
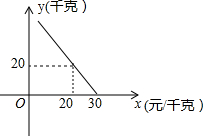 某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示. 如图,平面直角坐标系中,点A的坐标(-3,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD
如图,平面直角坐标系中,点A的坐标(-3,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD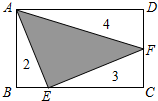 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为7.
如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为7.
 如图是正方体的一种展开图,其中每个面上都有一个数字,那么在原正方体中,与数字6相对面上的数字是( )
如图是正方体的一种展开图,其中每个面上都有一个数字,那么在原正方体中,与数字6相对面上的数字是( )