题目内容
16. 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )| A. | 10分钟 | B. | 15分钟 | C. | 20分钟 | D. | 25分钟 |
分析 作MN⊥AB于点N,即可证明△ABM是等腰三角形,然后在直角△BMN中,求得BM和BN之间的关系,则AB与N的大小关系即可求得,从而求得时间.
解答  解:作MN⊥AB于点N.
解:作MN⊥AB于点N.
∵在直角△BMN中,∠MBN=90°-30°=60°,∠BMN=30°,
又∵∠MAN=90°-60°=30°,
∴∠AMN=60°,
∴∠MAB=∠AMB,
∴AB=BM,
∴BN=$\frac{1}{2}$BM,
又∵由A到B航行半小时,即30分钟,
∴由B到N是15分钟.
故选B.
点评 此题考查了方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
6. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.1米.若小宇的身高是1.7米,则假山AC的高度为17米.
综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.1米.若小宇的身高是1.7米,则假山AC的高度为17米.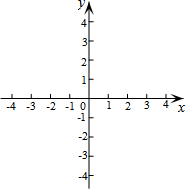 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-1,3),B(-3,2),C(0,1).画出△ABC,并画出关于原点O对称的△A1B1C1.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-1,3),B(-3,2),C(0,1).画出△ABC,并画出关于原点O对称的△A1B1C1. 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有两个不相等的实数根,则整数m的最小值为( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有两个不相等的实数根,则整数m的最小值为( )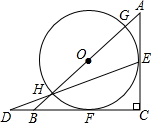 如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D.
如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D. 实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm).现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,则开始注入$\frac{3}{5}$,$\frac{33}{20}$,$\frac{171}{40}$分钟的水量后,甲与乙的水位高度之差是0.5cm.
实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm).现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm,则开始注入$\frac{3}{5}$,$\frac{33}{20}$,$\frac{171}{40}$分钟的水量后,甲与乙的水位高度之差是0.5cm.