题目内容
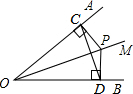 如图,已知OM为∠AOB的平分线,P为OM上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD,请指出图中有几个等腰三角形,并简要说明理由.
如图,已知OM为∠AOB的平分线,P为OM上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD,请指出图中有几个等腰三角形,并简要说明理由.考点:角平分线的性质,等腰三角形的判定
专题:
分析:根据角平分线性质求出PC=PD,根据勾股定理求出OC=OD,即可得出答案.
解答:解:有2个等腰三角形,是△COD,△PCD,
理由是:∵OM为∠AOB的平分线,P为OM上一点,PC⊥OA,PD⊥OB,
∴PC=PD,∠PCO=∠PDO=90°,
在Rt△PCO和Rt△PDO中,由勾股定理得:OC2=OP2-PC2,OD2=OP2-PD2,
∵PC=PD,OP=OP,
∴OC=OD,
即△COD,△PCD都是等腰三角形.
理由是:∵OM为∠AOB的平分线,P为OM上一点,PC⊥OA,PD⊥OB,
∴PC=PD,∠PCO=∠PDO=90°,
在Rt△PCO和Rt△PDO中,由勾股定理得:OC2=OP2-PC2,OD2=OP2-PD2,
∵PC=PD,OP=OP,
∴OC=OD,
即△COD,△PCD都是等腰三角形.
点评:本题考查了勾股定理,角平分线性质,等腰三角形的判定的应用,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目
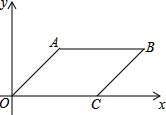 如图,已知平行四边形ABCO的四个顶点坐标分别是A(
如图,已知平行四边形ABCO的四个顶点坐标分别是A(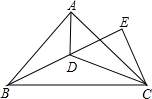 如图,BD、CD平分∠ABC、∠ACB,CE⊥BD交BD延长线于点E,求证:∠DCE=∠CAD.
如图,BD、CD平分∠ABC、∠ACB,CE⊥BD交BD延长线于点E,求证:∠DCE=∠CAD. 如图,BD,AH分别是△ABC的高,求证:A、B、H、D四点共圆.
如图,BD,AH分别是△ABC的高,求证:A、B、H、D四点共圆. 如图,△ABC内接于圆O,AD为BC边上的高,若AB=4cm,AC=3cm,AD=2.5cm,求圆O的半径.
如图,△ABC内接于圆O,AD为BC边上的高,若AB=4cm,AC=3cm,AD=2.5cm,求圆O的半径.