题目内容
 如图,BD,AH分别是△ABC的高,求证:A、B、H、D四点共圆.
如图,BD,AH分别是△ABC的高,求证:A、B、H、D四点共圆.考点:四点共圆
专题:证明题
分析:取AB的中点O,连接DO、HO,根据BD,AH分别是△ABC的高,可得△DAB和△HAB都是直角三角形,斜边都是AB,而点O为斜边中点,则有DO=HO=
AB=AO=BO,也就是说以O为圆心、OA为半径的圆,点D、H、B也在这个圆上,即可证明A、B、H、D四点共圆.
| 1 |
| 2 |
解答:证明:取AB的中点O,连接DO、HO,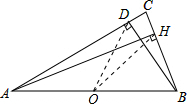
∵BD,AH分别是△ABC的高,
∴△DAB和△HAB都是直角三角形,且它们的斜边都是AB,
∵点O为斜边中点,
∴DO=HO=
AB=AO=BO,
也就是说,点D、H、B在以O为圆心、OA为半径的圆上,
即点D、H、B、A都在以O为圆心、以OA为半径的圆上,
故可得:A、B、H、D四点共圆.

∵BD,AH分别是△ABC的高,
∴△DAB和△HAB都是直角三角形,且它们的斜边都是AB,
∵点O为斜边中点,
∴DO=HO=
| 1 |
| 2 |
也就是说,点D、H、B在以O为圆心、OA为半径的圆上,
即点D、H、B、A都在以O为圆心、以OA为半径的圆上,
故可得:A、B、H、D四点共圆.
点评:本题考查了四点共圆,解答本题的关键是根据直角三角形斜边上的中线等于斜边的一半证得DO=HO=
AB=AO=BO,从而证明四点共圆.
| 1 |
| 2 |

练习册系列答案
相关题目
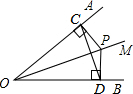 如图,已知OM为∠AOB的平分线,P为OM上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD,请指出图中有几个等腰三角形,并简要说明理由.
如图,已知OM为∠AOB的平分线,P为OM上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD,请指出图中有几个等腰三角形,并简要说明理由.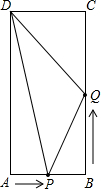 如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.
如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动. 若矩形CDEF相似于矩形ABCD,已知AB=4,BC=8,求矩形CDEF的宽DE.
若矩形CDEF相似于矩形ABCD,已知AB=4,BC=8,求矩形CDEF的宽DE.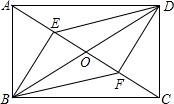 如图,在平行四边形ABCD中,∠ABC=90°,对角线AC与BD交于点O,BE⊥AC于E,DF⊥AC于F.
如图,在平行四边形ABCD中,∠ABC=90°,对角线AC与BD交于点O,BE⊥AC于E,DF⊥AC于F.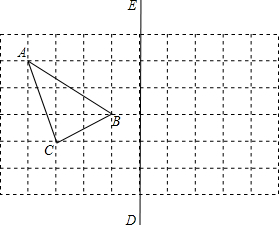 如图所示,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
如图所示,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)