题目内容
在Rt△ABC中,a、b、c分别是角A、B、C的对边,∠C=90°,∠B=30°,b+c=12,求a、b、c的值.
考点:含30度角的直角三角形,勾股定理
专题:
分析:根据含30度角的直角三角形性质得出c=2b,求出b的值,求出c的值,根据勾股定理求出a即可.
解答:
解:∵在Rt△ABC中,a、b、c分别是角A、B、C的对边,∠C=90°,∠B=30°,
∴c=2b,
∵b+c=12,
∴3b=12,
∴b=4,
∴c=2b=8,
由勾股定理得:a=
=
=4
.

解:∵在Rt△ABC中,a、b、c分别是角A、B、C的对边,∠C=90°,∠B=30°,
∴c=2b,
∵b+c=12,
∴3b=12,
∴b=4,
∴c=2b=8,
由勾股定理得:a=
| c2-b2 |
| 82-42 |
| 3 |
点评:本题考查了含30度角的直角三角形,勾股定理的应用,主要考查学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AC是⊙O的直径,AB、CD是⊙O的弦,且AB∥CD,图中有哪些角等于
如图,AC是⊙O的直径,AB、CD是⊙O的弦,且AB∥CD,图中有哪些角等于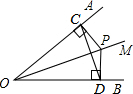 如图,已知OM为∠AOB的平分线,P为OM上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD,请指出图中有几个等腰三角形,并简要说明理由.
如图,已知OM为∠AOB的平分线,P为OM上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD,请指出图中有几个等腰三角形,并简要说明理由.