题目内容
如图，△ABC内接于圆O，AD为BC边上的高，若AB=4cm，AC=3cm，AD=2.5cm，求圆O的半径．考点：圆周角定理,相似三角形的判定与性质
专题：
分析：作直径AE，连接BE，根据圆周角定理得出∠C=∠E，∠AEC=90°，得出∠ABE=∠ADC=90°，从而得出△ACD∽△AEB，得出对应边成比例即可得出直径AE，进而求得半径．
解答：
解：作直径AE，连接BE，
∴∠C=∠E，
∵AD⊥BC，AE是直径，
∴∠ABE=∠ADC=90°，
∴△ACD∽△AEB，
∴
=
，
即
=
，解得，AE=
，
∴圆O的半径为
．
解：作直径AE，连接BE，∴∠C=∠E，
∵AD⊥BC，AE是直径，
∴∠ABE=∠ADC=90°，
∴△ACD∽△AEB，
∴
| AE |
| AC |
| AB |
| AD |
即
| AE |
| 3 |
| 4 |
| 2.5 |
| 24 |
| 5 |
∴圆O的半径为
| 12 |
| 5 |
点评：本题考查了圆周角定理的应用，三角形系数的判定和性质，熟练掌握性质和定理是本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
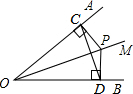如图，已知OM为∠AOB的平分线，P为OM上一点，PC⊥OA于点C，PD⊥OB于点D，连接CD，请指出图中有几个等腰三角形，并简要说明理由．
若矩形CDEF相似于矩形ABCD，已知AB=4，BC=8，求矩形CDEF的宽DE．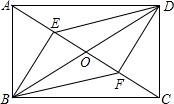
如图，在平行四边形ABCD中，∠ABC=90°，对角线AC与BD交于点O，BE⊥AC于E，DF⊥AC于F．
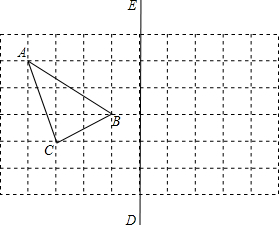如图所示，在所给正方形网格图中完成下列各题：（用直尺画图，保留痕迹）