题目内容
14.闵行体育公园的圆形喷水池的水柱(如图1)如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度)y(米)关于水平距离x(米)的函数解析式为y=-x2+4x+$\frac{9}{4}$,那么圆形水池的半径至少为$\frac{9}{2}$米时,才能使喷出的水流不落在水池外.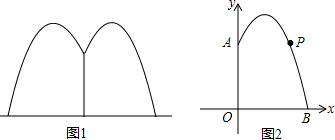
分析 根据二次函数的解析式求得抛物线与x轴的交点坐标的横坐标,即为所求的结果.
解答 解:当y=0时,即-x2+4x+$\frac{9}{4}$=0,
解得x1=$\frac{9}{2}$,x2=-$\frac{1}{2}$(舍去).
答:水池的半径至少$\frac{9}{2}$米时,才能使喷出的水流不落在水池外.
故答案为:$\frac{9}{2}$.
点评 本题考查了二次函数的应用,注意抛物线的解析式的三种形式在解决抛物线的问题中的作用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.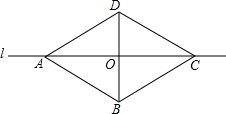 如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
 如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )| A. | ①②③④ | B. | ①③④ | C. | ②③④ | D. | ③④ |
 如图是由边长为1的小正方形组成的方格图.
如图是由边长为1的小正方形组成的方格图. 如图,A,B,C这三个点表示三个工厂,它们在同一个圆上,要建立一个供水站,使它到这三个工厂的距离相等,请找出供水站的位置.
如图,A,B,C这三个点表示三个工厂,它们在同一个圆上,要建立一个供水站,使它到这三个工厂的距离相等,请找出供水站的位置. 如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.
如图已知直线$y=-\frac{{\sqrt{3}}}{3}x+1$与x轴和y轴分别交于点A和点B,以AB为边在第一象限内作等边三角形ABC.