题目内容
 平行四边形中,相邻两条边长分别为5米和6米,一条对角线长为8米,另一条对角线为
平行四边形中,相邻两条边长分别为5米和6米,一条对角线长为8米,另一条对角线为| k |
考点:平行四边形的性质
专题:
分析:首先过点C作CF⊥AB于点F,作DE⊥AB于点E,由勾股定理可得DE2=BD2-BE2=DA2-AE2,则可求得AE的长,继而求得DE2的值,易证得△BCF≌△ADE(AAS),可得BF=AE=
,CF=DE,然后由AC2=CF2+AF2,求得答案.
| 1 |
| 4 |
解答: 解:过点C作CF⊥AB于点F,作DE⊥AB于点E,
解:过点C作CF⊥AB于点F,作DE⊥AB于点E,
∵DE2=BD2-BE2=DA2-AE2,
∴82-(6+AE)2=52-AE2,
解得:AE=
,
∴DE2=24
,
∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∴∠CBF=∠DAE,
在△BCF和△ADE中,
,
∴△BCF≌△ADE(AAS),
∴BF=AE=
,CF=DE,
∴AF=AB-AF=6-
=
,
∵AC2=CF2+AF2,
∴k=58.
 解:过点C作CF⊥AB于点F,作DE⊥AB于点E,
解:过点C作CF⊥AB于点F,作DE⊥AB于点E,∵DE2=BD2-BE2=DA2-AE2,
∴82-(6+AE)2=52-AE2,
解得:AE=
| 1 |
| 4 |
∴DE2=24
| 15 |
| 16 |
∵四边形ABCD是平行四边形,
∴BC=AD,BC∥AD,
∴∠CBF=∠DAE,
在△BCF和△ADE中,
|
∴△BCF≌△ADE(AAS),
∴BF=AE=
| 1 |
| 4 |
∴AF=AB-AF=6-
| 1 |
| 4 |
| 23 |
| 4 |
∵AC2=CF2+AF2,
∴k=58.
点评:此题考查了平行四边形的性质、全等三角形的判定与性质以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图所示,∠AOB=90°,∠COD=90°,∠AOD=
如图所示,∠AOB=90°,∠COD=90°,∠AOD= 如图所示,AC,BD是⊙O的两条直径,连接AD,BC,请你判断四边形ABCD的形状并说明道理.
如图所示,AC,BD是⊙O的两条直径,连接AD,BC,请你判断四边形ABCD的形状并说明道理. 已知,如图,在△ABC中,∠ACB=90°,CB=6,AB=12,求∠A,∠B的度数.
已知,如图,在△ABC中,∠ACB=90°,CB=6,AB=12,求∠A,∠B的度数. 如图,AM是△ABC外接圆的直径,△ABC的高AD的延长线交圆O于点N,求证:BN=CM.
如图,AM是△ABC外接圆的直径,△ABC的高AD的延长线交圆O于点N,求证:BN=CM. 某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元.
某市在“旧城改造”中,计划在市内一块如图所示的三角形空地中种植草皮美化环境,已知这种草皮每平方米要80元,求买这种草皮至少需多少元. 如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,E是AC的中点,若DE=2,CD=2
如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,E是AC的中点,若DE=2,CD=2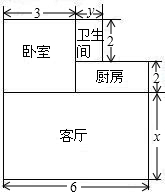 大伟购买了一套经济适用房,户型图如图所示,请根据图中的数据(单位:m),解答下列问题:
大伟购买了一套经济适用房,户型图如图所示,请根据图中的数据(单位:m),解答下列问题: