题目内容
 已知,如图,在△ABC中,∠ACB=90°,CB=6,AB=12,求∠A,∠B的度数.
已知,如图,在△ABC中,∠ACB=90°,CB=6,AB=12,求∠A,∠B的度数.考点:含30度角的直角三角形
专题:
分析:先在△ABC中,由正弦函数的定义得出sin∠A=
=
=
,根据特殊角的三角函数值得到∠A=30°,再根据直角三角形两锐角互余即可求出∠B=90°-∠A=60°.
| BC |
| AB |
| 6 |
| 12 |
| 1 |
| 2 |
解答:解:∵在△ABC中,∠ACB=90°,CB=6,AB=12,
∴sin∠A=
=
=
,
∴∠A=30°,
∴∠B=90°-∠A=60°.
∴sin∠A=
| BC |
| AB |
| 6 |
| 12 |
| 1 |
| 2 |
∴∠A=30°,
∴∠B=90°-∠A=60°.
点评:本题考查了解直角三角形,特殊角的三角函数值,直角三角形两锐角互余的性质,比较简单.求出sin∠A=
是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
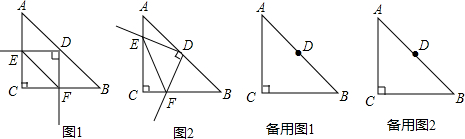
 如图,四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD是平行四边形.
如图,四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD是平行四边形. 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,若AD=1,BC=3,则S△AOD:S△BOC的值为
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,若AD=1,BC=3,则S△AOD:S△BOC的值为 平行四边形中,相邻两条边长分别为5米和6米,一条对角线长为8米,另一条对角线为
平行四边形中,相邻两条边长分别为5米和6米,一条对角线长为8米,另一条对角线为 如图,完成下列填空:
如图,完成下列填空: 如图,在正六边形ABCDEF(各边相等,各角相等)中,△DOE可以由
如图,在正六边形ABCDEF(各边相等,各角相等)中,△DOE可以由