题目内容
13. 已知直线a∥b,直线c分别与直线a、b相交,∠l=(4x-5)°,∠2=(x+35)°,求∠1、∠2的度数.
已知直线a∥b,直线c分别与直线a、b相交,∠l=(4x-5)°,∠2=(x+35)°,求∠1、∠2的度数.
分析 先根据对顶角相等,得出∠1=∠3,∠2=∠4,再根据平行线的性质,得出(4x-5)°+(x+35)°=180°,进而解得x=30°,最后得出∠1、∠2的度数.
解答  解:∵直线c分别与直线a、b相交,
解:∵直线c分别与直线a、b相交,
∴∠1=∠3,∠2=∠4,
又∵a∥b,
∴∠3+∠4=∠1+∠2=180°,
又∵∠l=(4x-5)°,∠2=(x+35)°,
∴(4x-5)°+(x+35)°=180°,
解得x=30°,
∴∠l=(4x-5)°=115°,∠2=(x+35)°=65°.
点评 本题主要考查了平行线的性质以及对顶角相等的运用,解决问题的关键是掌握:两直线平行,同旁内角互补.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.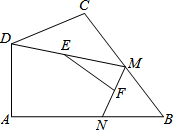 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{7}$ |
5.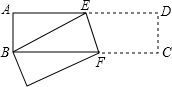 如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
 如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | $3\sqrt{3}$ |
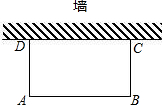 如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,怎样围才能使矩形场地的面积为750m2?
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,怎样围才能使矩形场地的面积为750m2? 如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.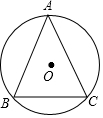 已知⊙O的半径为2,△ABC内接于⊙O,$\widehat{AB}$、$\widehat{BC}$、$\widehat{AC}$的长之比为3:2:3,求BC的长.
已知⊙O的半径为2,△ABC内接于⊙O,$\widehat{AB}$、$\widehat{BC}$、$\widehat{AC}$的长之比为3:2:3,求BC的长. 如图,将字母“V”向右平移2格会得到字母“W”.
如图,将字母“V”向右平移2格会得到字母“W”.