题目内容
18．四川雅安地震期间，为了紧急安置60名地震灾民，需要搭建可容纳6人或4人的帐篷，若所搭建的帐篷恰好（即不多不少）能容纳这60名灾民，则不同的搭建方案有（ ）| A． | 4种 | B． | 11种 | C． | 6种 | D． | 9种 |
分析 设6人帐篷用了x个，4人帐篷用了y个，根据题意列出方程，求出方程的解即可得到结果．
解答 解：设6人帐篷用了x个，4人帐篷用了y个，
根据题意得：6x+4y=60，即y=$\frac{60-6x}{4}$=$\frac{30-3x}{2}$，
当x=0时，y=15；
当x=2时，y=12；
当x=4时，y=9；
当x=6，y=6；
当x=8时，y=3；
当x=10时，y=0；
则不同的搭建方案有6种．
故选：C．
点评 此题考查了二元一次方程的应用．
（1）找出问题中的已知条件和未知量及它们之间的关系．
（2）找出题中的两个关键的未知量，并用字母表示出来．
（3）挖掘题目中的关系，找出等量关系，列出二元一次方程．
（4）根据未知数的实际意义求其整数解．
练习册系列答案
相关题目
8．
下列不等式组的解集，在数轴上表示为如图所示的是（ ）
下列不等式组的解集，在数轴上表示为如图所示的是（ ）| A． | $\left\{\begin{array}{l}{x-1＞0}\\{x+2≤0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+1＞0}\\{x-2≤0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+1≥0}\\{x-2＜0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x-1≤0}\\{x+2＜0}\end{array}\right.$ |
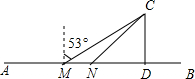重庆市铜梁区政府为做大乡村旅游，打造了“五朵金花”，其中西边A处有“万亩生态湿地荷花园”，东边B处有“沙心玫瑰园”，为了落实这一举措，区政府计划在A、B两旅游景点之间修建一条公路AB，已知公路AB的一侧有“四季花海”景点C，在公路AB上的M处测得景点C在M的北偏东53°方向上，从M向东走300米到达N处，测得景点C在N的东北方向上，且景点C周围800米范围内为“四季花海”．
3．设a、b是方程x2-12x+9=0的两个根，则$\sqrt{a}+\sqrt{b}$等于（ ）
| A． | 18 | B． | $\sqrt{6}$ | C． | $3\sqrt{2}$ | D． | ±$3\sqrt{2}$ |
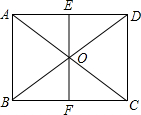如图，?ABCD中，O是对角线AC、BD的交点，AB=4cm，BC=5cm，则?ABCD的周长是18cm；若EF过O交AD于E，交BC于F，OE=2cm，则OF=2cm，四边形ABFE的周长是13cm．
如图，AB是⊙O的弦，OC⊥AB，垂足为C．若AB=2$\sqrt{3}$，OC=1，则OB的长为2．