题目内容
3.设a、b是方程x2-12x+9=0的两个根,则$\sqrt{a}+\sqrt{b}$等于( )| A. | 18 | B. | $\sqrt{6}$ | C. | $3\sqrt{2}$ | D. | ±$3\sqrt{2}$ |
分析 先根据根与系数的关系得到a+b=12,ab=9,再计算($\sqrt{a}$+$\sqrt{b}$)2的值,然后利用算术平方公式的定义求解.
解答 解:根据题意得a+b=12,ab=9,
所以($\sqrt{a}$+$\sqrt{b}$)2=a+b+2$\sqrt{ab}$=12+2×$\sqrt{9}$=18,
而$\sqrt{a}$+$\sqrt{b}$>0,
所以$\sqrt{a}$+$\sqrt{b}$=$\sqrt{18}$=3$\sqrt{2}$.
故选C.
点评 本题考查了根与系数的关系:二次项系数不为1,则常用以下关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
11.函数$y=\frac{x}{x-1}$中自变量x的取值范围是( )
| A. | x>1 | B. | x>0 | C. | x≠0 | D. | x≠1 |
13. 如图两个三角形是位似图形,它们的位似中心是( )
如图两个三角形是位似图形,它们的位似中心是( )
 如图两个三角形是位似图形,它们的位似中心是( )
如图两个三角形是位似图形,它们的位似中心是( )| A. | 点P | B. | 点O | C. | 点M | D. | 点N |
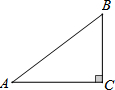 如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm
如图,△ABC中∠ACB=90°,AC=8cm,BC=6cm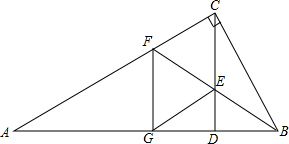 如图:BF是Rt△ABC的角平分线,∠ACB=90°,CD是高,BF与CD交于点E,EG∥AC交AB于G.求证:FG⊥AB.
如图:BF是Rt△ABC的角平分线,∠ACB=90°,CD是高,BF与CD交于点E,EG∥AC交AB于G.求证:FG⊥AB.