Question

7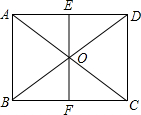．如图，?ABCD中，O是对角线AC、BD的交点，AB=4cm，BC=5cm，则?ABCD的周长是18cm；若EF过O交AD于E，交BC于F，OE=2cm，则OF=2cm，四边形ABFE的周长是13cm．

Answer 1

分析 利用平行四边形的性质进而得出?ABCD的周长，再求出△AOE≌△COF得出EO=FO=2cm，进而得出四边形ABFE的周长．

解答 解：∵四边形ABCD是平行四边形，
∴AB=DC=4cm，AD=BC=5cm，
∴?ABCD的周长是18cm，
∵四边形ABCD是平行四边形，
∴AO=CO，∠OAE=∠OCB，
在△AOE和△COF中
∵$\left\{\begin{array}{l}{∠AO=∠FCO}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$，
∴△AOE≌△COF（ASA），
∴EO=FO=2cm，
∴AE=FC，
∴四边形ABFE的周长是：AB+AE+BF+EO+FO=AB+BC+4=4+5+4=13（cm）．
故答案为：18cm，2cm，13cm．

点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质，得出△AOE≌△COF是解题关键．