题目内容
8. 如图,AB是⊙O的弦,OC⊥AB,垂足为C.若AB=2$\sqrt{3}$,OC=1,则OB的长为2.
如图,AB是⊙O的弦,OC⊥AB,垂足为C.若AB=2$\sqrt{3}$,OC=1,则OB的长为2.
分析 先根据垂径定理得出BC的长,再在Rt△OBC中利用勾股定理求出OB的长即可.
解答 解:∵AB是⊙O的弦,OC⊥AB于C,AB=$2\sqrt{3}$,
∴BC=$\frac{1}{2}$AB=$\sqrt{3}$,
∵0C=1,
∴在Rt△OBC中,
OB=$\sqrt{O{C}^{2}+B{C}^{2}\\;}=\sqrt{{1}^{2}+(\sqrt{3})^{2}}=2$.
故答案为:2.
点评 本题考查的是垂径定理及勾股定理,先求出BC的长,再利用勾股定理求出OB的长是解答此题的关键.

练习册系列答案
相关题目
13. 如图两个三角形是位似图形,它们的位似中心是( )
如图两个三角形是位似图形,它们的位似中心是( )
 如图两个三角形是位似图形,它们的位似中心是( )
如图两个三角形是位似图形,它们的位似中心是( )| A. | 点P | B. | 点O | C. | 点M | D. | 点N |
18.老王家上个月付话费31元,其月租费为21元,已知市内电话不超过3分钟,每次花费0.18元,如果老王家每次电话不超过3分钟,则老王家至多打电话( )
| A. | 55次 | B. | 56次 | C. | 57次 | D. | 58次 |
 如图,过?ABCD对角线AB、BD的交点O作一直线,分别交AB和DC于E、F,交CB和AD的延长线于G、H,求证:DH=BG.
如图,过?ABCD对角线AB、BD的交点O作一直线,分别交AB和DC于E、F,交CB和AD的延长线于G、H,求证:DH=BG.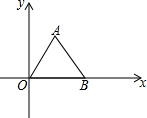 如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$.
如图,A,B两点的坐标分别是A(1,$\sqrt{3}$),B($\sqrt{5}$,0),则△ABO的面积是$\frac{\sqrt{15}}{2}$.